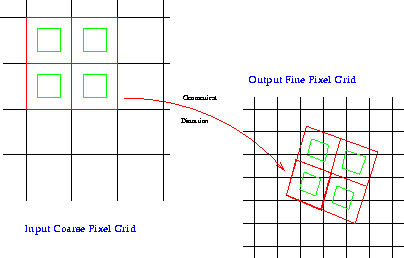
Figure: A Schematic representation of drizzling. Original PostScript figure (8kB).
Next: Heuristic Estimates of Weighted Binomial Statistics for Use in Detecting Rare Point Source Transients
Previous: RoadRunner: An Automated Reduction System for Long Slit Spectroscopic Data
Up: Algorithms
Table of Contents - Index - PS reprint
Richard N. Hook
Space Telescope - European Coordinating Facility, European Southern
Observatory, Karl Schwarzschild Str.-2, D-85748, Garching, Germany,
E-mail: rhook@eso.org
Andrew S. Fruchter
Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218, USA, E-mail: fruchter@stsci.edu
Many imaging systems in astronomy have detectors which undersample the image that falls on them. An important example, which we consider here, is the Wide Field Planetary Camera 2 (WFPC2) on the Hubble Space Telescope (HST). Although the optics of WFPC2 provide a superb Point Spread Function (PSF), the detectors at the focal plane severely undersample the image. This problem is most acute for the three WF chips, where the width of a pixel equals the FWHM of the optics in the near-infrared, and greatly exceeds it in the blue.
Much of the information lost in sampling can be recovered by combining images which have been shifted by fractions of a pixel between successive exposures. Such images are referred to as ``dithered,'' and this observing strategy is commonly used with WFPC2. Several methods have been proposed for such a combination, including methods based on iterative, maximum likelihood reconstruction methods. Such methods can be effective but tend to be slow and unable to handle effectively geometrically distorted images such as those produced by WFPC2. They also produce images in which the noise properties are correlated from pixel to pixel and the statistical errors are difficult to estimate. To avoid these problems, and to handle the major image combination problem posed by the ``Hubble Deep Field'' (HDF, Williams et al. 1996), we have considered the family of techniques we refer to as ``linear reconstruction.'' The most commonly used of these techniques are shift-and-add and interlacing. However, due to poor placement of the sampling grid or the effects of geometric distortion, true interlacing of images is often not feasible. On the other hand, the other standard technique, shift-and-add, convolves the image yet again with the original pixel, further adding to the blurring of the image. Here we present a method which has the versatility of shift-and-add and yet aims to maintain the resolution of interlacing.
``Drizzling'' maps pixels in the original input images onto the pixel grid of a subsampled output image, taking into account shifts and rotations between images and the optical distortion of the camera. However, in order to avoid convolving the image with the large pixel ``footprint'' of the camera, we allow the user to shrink the pixel before it is averaged into the output image. The new shrunken pixels, or ``drops,'' rain down upon the subsampled output image. In the case of HST/WFPC2 images with multiple dither positions (such as the Hubble Deep Field), the drops typically have linear dimensions one-half that of the input pixel-slightly larger than the size chosen for the output subsampled pixels. The flux in each drop is divided up among the overlapping output pixels with weights proportional to the areas of overlap. This procedure is shown schematically in Figure 1. Note that if the drop size is sufficiently small not all output pixels have any data added to them from an input image. A drop size must therefore be chosen that is small enough to minimize degradation of spatial resolution but large enough that the coverage is fairly uniform after all the images have been drizzled.

Figure: A Schematic representation of drizzling.
Original PostScript figure (8kB).
When a drop with value
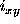 and user defined weight
and user defined weight 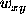 is added to an image with pixel value
is added to an image with pixel value
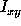 , weight
, weight 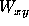 , and fractional pixel overlap
, and fractional pixel overlap
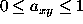 , the resulting value of the image
, the resulting value of the image 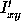 and weight
and weight 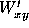 is
is
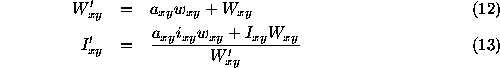
This algorithm preserves both surface and absolute photometry so that flux density can be measured using an aperture whose size is independent of position on the chip. The weighting arrays also allow missing data, due to cosmic ray hits and hot pixels, to be handled in a totally flexible way. The linear weighting scheme employed is statistically optimum when inverse variance maps are used as weights. These weights may vary spatially to accommodate changing signal-to-noise ratios across input frames (e.g., due to variable scattered light). The final output weighting image (an inverse variance map) is saved as well as the combined image frame and can be used in further analysis.
The method also minimizes resolution loss, and largely eliminates the distortion of absolute photometry produced by the flat-fielding of the geometrically distorted images (see § 4).
To obtain more information about the drizzling method, as well as a well-tested version of the software which will run under IRAF, the drizzling Webpage should be consulted.
The drizzling algorithm was designed to obtain optimal signal-to-noise on faint objects while preserving image resolution. These goals are, unfortunately, not fully compatible. For example, non-linear image restoration procedures which attempt to remove the blurring of the PSF and the pixel by enhancing the high frequencies in the image (such as such as the Richardson-Lucy and MEM methods) directly exchange signal-to-noise for resolution. In the drizzling algorithm, no compromises on signal-to-noise have been made, and the weight of an input pixel in the final output image is entirely independent of its position on the chip. Therefore, if the dithered images do not uniformly sample the field, the ``center of light'' in an output pixel may be offset from the center of the pixel, and that offset may vary between adjacent pixels. This effect is seen in the HDF images, where some pointings were not at the requested position or orientation. Furthermore, large dithering offsets which may be used for WFPC2 imaging, combined with geometric distortion, produce a sampling pattern that varies across the field. The output PSFs produced by the combination of such irregularly dithered datasets using drizzling may show substantial variations about the best fit Gaussian due to the effects of non-uniform sampling. Fortunately, these variations do not noticeably affect aperture photometry performed with typical aperture sizes.
The WFPC2 optics geometrically distort the images: pixels at the corner of each CCD subtend less area on the sky than those near the center. However, after application of the flat field, a source of uniform surface brightness on the sky produces uniform counts across the CCD. Therefore point sources near the corners of the chip are artificially brightened compared to those in the center.
This effect has been studied by performing photometry on a grid of 19×19 artificial stellar PSFs which had their counts adjusted to reflect the effect of geometric distortion-the stars in the corners are up to ~4% brighter than those in the center of the chip. This image was then shifted and sampled on a 2×2 grid and the results combined using drizzling and typical parameters. Aperture photometry on the 19×19 grid after drizzling reveals that the effect of geometric distortion on the photometry has been dramatically reduced: the RMS photometric variation in the drizzled image is 0.004 magnitudes.
Few HST observing proposals have sufficient time to take multiple exposures at each of several dither positions. So if dithering is to be of widespread use, one must be able to remove cosmic rays from data where few, if any, images are taken at the same position on the sky. We have therefore been examining the question of whether we can adapt the drizzling procedure to the removal of cosmic rays. Although the removal of cosmic rays using drizzling is still very much work in progress, we have developed a procedure which appears quite promising. Figure 2 shows the result of such processing on a set of twelve dithered deep WFPC2 images taken from the archive.

Figure: Cosmic ray removal on dithered images using drizzling
Original PostScript figure (656kB).
Williams, R. E., et al. 1996, AJ, 112, 1335
Next: Heuristic Estimates of Weighted Binomial Statistics for Use in Detecting Rare Point Source Transients
Previous: RoadRunner: An Automated Reduction System for Long Slit Spectroscopic Data
Up: Algorithms
Table of Contents - Index - PS reprint