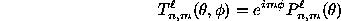
Next: Image Reconstruction with Few Strip-Integrated Projections:
Enhancements by Application of Versions of the CLEAN Algorithm
Previous: Titan Image Processing
Up: Algorithms
Table of Contents - Index - PS reprint
P. B. Keegstra1, C. L. Bennett2,
G. F. Smoot3, K. M. Gorski4,
G. Hinshaw2, L. Tenorio5
1Hughes STX Corporation
2Laboratory for Astronomy and Solar Physics,
NASA/Goddard Space Flight Center
3Lawrence Berkeley Laboratory, University of California,
Berkeley
4Theoretical Astrophysics Center, Denmark and
Warsaw University Observatory, Poland
5Universidad Carlos III de Madrid, Spain
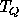 and
and 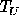 , as in analyzing
polarization results
from the Differential Microwave Radiometers (DMR) on
NASA's Cosmic Background Explorer ( COBE ),
coordinate transformations produce a mixing of
, as in analyzing
polarization results
from the Differential Microwave Radiometers (DMR) on
NASA's Cosmic Background Explorer ( COBE ),
coordinate transformations produce a mixing of 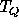 and
and 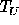 .
Consequently, it is inappropriate
to expand
.
Consequently, it is inappropriate
to expand 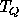 and
and 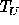 in ordinary spherical harmonics. The proper
expansion expresses both
in ordinary spherical harmonics. The proper
expansion expresses both 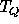 and
and 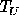 simultaneously in terms of
a particular order of generalized spherical harmonics.
The approach described here has been implemented, and is being used
to analyze the polarization signals from the DMR data.
simultaneously in terms of
a particular order of generalized spherical harmonics.
The approach described here has been implemented, and is being used
to analyze the polarization signals from the DMR data.
Generalized spherical harmonics are an extension of ordinary spherical harmonics, intended for expansion of functions whose transformation properties at each point on the sphere are more complex than just scalars. The general form
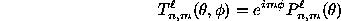
has three indices 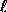 , m, and n where
, m, and n where
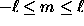 and
and
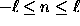 (Gel'fand et al. 1963).
The forms appropriate for expanding complex Stokes
parameters
(Gel'fand et al. 1963).
The forms appropriate for expanding complex Stokes
parameters 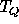 and
and 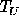 are (Sazhin & Korolëv 1985)
are (Sazhin & Korolëv 1985)
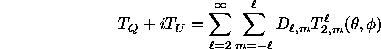
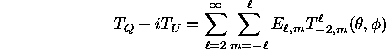
Since  and
and  are real and
are real and
 , the two expansions
are degenerate, and we may restrict our consideration
to the first form.
Thus, for the DMR case we need only consider
generalized spherical harmonics with n=2,
which we will henceforth refer to as
, the two expansions
are degenerate, and we may restrict our consideration
to the first form.
Thus, for the DMR case we need only consider
generalized spherical harmonics with n=2,
which we will henceforth refer to as 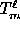 .
.
The 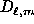 are complex expansion coefficients, analogues of
the
are complex expansion coefficients, analogues of
the 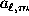 of ordinary spherical harmonic expansions of
scalar quantities. Like them, the
of ordinary spherical harmonic expansions of
scalar quantities. Like them, the 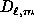 for a given
for a given
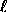 transform among themselves in a coordinate transformation,
but the absolute sum
transform among themselves in a coordinate transformation,
but the absolute sum 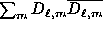 is invariant.
is invariant.
Following recent work by Zaldarriaga & Seljak (1997)
and Kamionkowski et al. (1997), we can partition
the 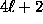 independent real parameters per value of
independent real parameters per value of 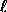 into those associated with even-parity solutions and odd-parity
solutions, called E-like and B-like respectively by Zaldarriaga
& Seljak. The formula appropriate for the phase convention used
here is
into those associated with even-parity solutions and odd-parity
solutions, called E-like and B-like respectively by Zaldarriaga
& Seljak. The formula appropriate for the phase convention used
here is
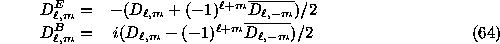
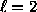 , and
for each
, and
for each 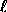 ,
, 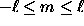 .
.
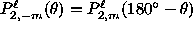 .
.
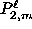 is real for m even, and pure imaginary
for m odd.
is real for m even, and pure imaginary
for m odd.
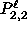 , which is
nonzero at the North Pole (
, which is
nonzero at the North Pole (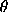 = 0°), and
= 0°), and 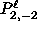 ,
nonzero at the South Pole (
,
nonzero at the South Pole (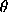 = 180°).
= 180°).
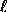 , the integral over the sphere
of the sum of squares for all m gives unity.
Thus the ``strength'' of an individual function decreases as
, the integral over the sphere
of the sum of squares for all m gives unity.
Thus the ``strength'' of an individual function decreases as
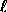 increases when contrasted with the usual
normalization for ordinary spherical harmonics, where each m
individually integrates to unity.
increases when contrasted with the usual
normalization for ordinary spherical harmonics, where each m
individually integrates to unity.
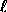 and then on m are used
to reach each particular function.
(Note that
and then on m are used
to reach each particular function.
(Note that 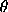 here refers
to the colatitude, not the latitude.)
here refers
to the colatitude, not the latitude.)
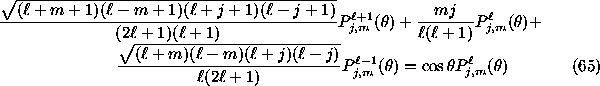
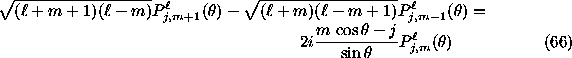
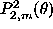 . (The recursion in
. (The recursion in 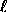 at
at 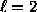 defines
defines 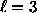 , since the coefficient
for
, since the coefficient
for 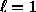 vanishes.)
vanishes.)
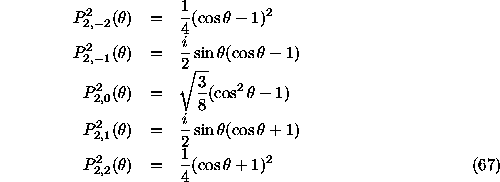
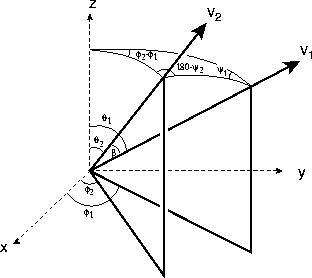
Figure: Geometry for definitions
of 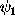 and
and 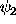 (Kosowsky 1996).
Original PostScript figure (48kB).
(Kosowsky 1996).
Original PostScript figure (48kB).
Generalized spherical harmonics obey a sum rule
analogous to a familiar one for ordinary spherical harmonics,
but it includes an explicit phase factor which depends
on the orientation of the two lines of sight.
That phase factor depends on the angle 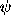 which
carries the reference direction for line of sight
which
carries the reference direction for line of sight 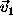 into the reference direction for line of sight
into the reference direction for line of sight 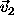 .
The geometry of
.
The geometry of 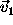 and
and 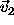 is illustrated
in Figure 1.
is illustrated
in Figure 1. 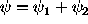 ,
which has the following geometric interpretation.
The reference direction is rotated by
,
which has the following geometric interpretation.
The reference direction is rotated by 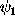 into the great circle from
into the great circle from 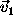 to
to 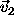 ,
translated to
,
translated to 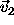 , and then rotated through
, and then rotated through 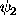 to bring it
into alignment with the reference direction at
to bring it
into alignment with the reference direction at 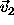 .
(
.
(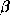 is the angle between
is the angle between 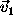 and
and 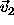 ).
).
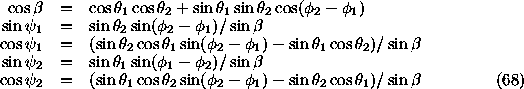
With that definition of  , the sum rule relating generalized
spherical harmonics along two lines of sight to
the angle
, the sum rule relating generalized
spherical harmonics along two lines of sight to
the angle 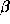 between those lines of sight is
between those lines of sight is
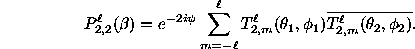
If this phase factor is included in the definition
of the spherical average
over all directions 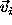 and
and 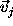 separated
by an angle
separated
by an angle 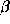
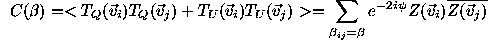
where 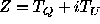 ,
then this allows us to define rotationally invariant
analogues
,
then this allows us to define rotationally invariant
analogues 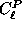 to the power spectra
to the power spectra 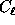 :
:
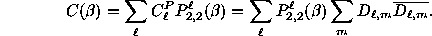
Additionally, we can construct analogous sums
of 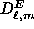 and
and 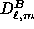 ,
which we denote as
,
which we denote as 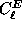 and
and 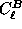 respectively.
These
are the appropriate quantities to use for
comparison to theoretical treatments of polarization.
The partitioning into
respectively.
These
are the appropriate quantities to use for
comparison to theoretical treatments of polarization.
The partitioning into 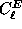 and
and 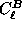 is
pertinent since Zaldarriaga & Seljak (1996)
and Kamionkowski et al. (1996) both show that
scalar perturbations cannot produce a nonzero
is
pertinent since Zaldarriaga & Seljak (1996)
and Kamionkowski et al. (1996) both show that
scalar perturbations cannot produce a nonzero 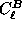 .
.
It is interesting to note that 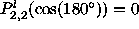 ,
which implies that correlations between physical polarization
signals vanish at the antipodes.
,
which implies that correlations between physical polarization
signals vanish at the antipodes.
The National Aeronautics and Space Administration (NASA)/Goddard Space Flight Center (GSFC) is responsible for the design, development, and operation of the Cosmic Background Explorer ( COBE ). Scientific guidance is provided by the COBE Science Working Group. GSFC is also responsible for the development of analysis software and for the production of the mission data sets.
Fruitful discussions with M. Jacobsen, University of Maryland Department of Mathematics, and B. Summey, Hughes STX, are gratefully acknowledged.
Gel'fand, I. M., Minlos, R. A., & Shapiro, Z. Y. 1963, Representations of the Rotation and Lorentz Groups and their Applications (New York: Pergamon Press)
Kamionkowski, M., Kosowsky, A., & Stebbins, A. 1997, Phys. Rev. Lett., 78, 2038
Kosowsky, A. 1996, Ann. Phys., 246, 49
Sazhin, M. V., & Korolëv, V. A. 1985, Sov. Astron. Lett., 11, 204
Zaldarriaga, M., & Seljak, U. 1997, Phys. Rev. D, in press
Next: Image Reconstruction with Few Strip-Integrated Projections:
Enhancements by Application of Versions of the CLEAN Algorithm
Previous: Titan Image Processing
Up: Algorithms
Table of Contents - Index - PS reprint