Next: Using Massively Parallel Processing of a NLTE Spectrum Synthetic Code and an Automated Comparison with Observations to Determine the Properties of Type Ia Supernovae from their Late Time Spectra.
Previous: Numerical Simulations of Plasmas and Their Spectra
Up: Modeling
Table of Contents - Index - PS reprint
Astronomical Data Analysis Software and Systems VI
ASP Conference Series, Vol. 125, 1997
Editors: Gareth Hunt and H. E. Payne
I. Stern
Smithsonian Astrophysical Observatory, Cambridge, MA 02138
Abstract:
Fractals and multifractals are used to model hierarchical, inhomogeneous
structures in several areas of astrophysics, notably the distribution of
matter at various scales in the universe. Current analysis techniques used
to assert fractality or multifractality and extract scaling exponents from
astrophysical data, however, have significant limitations and caveats.
It is pointed out that some of the difficulties regarding the convergence
rates of algorithms used to determine scaling exponents for a fractal
or multifractal, are intrinsically related to its texture, in particular,
to its lacunarity. A novel approach to characterize prefactors of
cover functions, in particular, lacunarity, based on the formalism of
regular variation (in the sense of Karamata) is proposed. This
approach allows deriving bounds on convergence rates for scaling
exponent algorithms and may provide more precise characterizations for
fractal-like objects of interest for astrophysics. An application of
regular variation based fractal modeling to apollonian packing, which
can be useful in cosmic voids morphology modeling, is also suggested.
Structures with fractal characteristics are important for astrophysics.
Fractal-like structures may be created whenever nonlinear dynamical mechanisms
are at work. Such mechanisms may generate inhomogeneity on a large range of
physical scales and ``incomplete space filling.'' For example, certain aspects of
the distribution of matter in the universe are well described by fractals at small
and medium scales (distribution of galaxy number counts, microwave background
fluctuations, etc.) (Borgani 1995). However, the problem of a crossover from
``fractality'' to ``homogeneity'' at large scales, as required by the cosmological
principle (Peebles 1993), raises some questions related to formal aspects of the
fractal modeling involved and the ways in which the data are analyzed (Labini
et al. 1996). At this point in time, it is recognized that fractal models with
pure scale invariance are not sufficient to describe the morphology of large
scale structure. In addition, the details of the mentioned crossover, if it
exists, are open. In fact, it was pointed out recently (Mandelbrot 1995) that
the research regarding the large scale morphology can benefit from a better
understanding of the finer morphological features of fractals, namely, of their
texture, and in particular, their lacunarity.
For a fractal, the fractal dimension alone is an incomplete description of the
degree and nature of space filling. One can generate fractals with exactly the
same fractal dimension and very different space filling structure or lacunarity.
In a family of fractals with the same fractal dimension, the lower the ``lacunarity''
of a fractal the closer its appearance is to ``homogeneity.'' Thus, as pointed out
by Mandelbrot, large scale homogeneity may be mimicked by a fractal structure with
low lacunarity (Mandelbrot 1983, 1995). Moreover, texture and even the fractal
dimension can change with scale (a structure can be fractal without being scale
invariant). The existence of ``transient fractals'' (for which the ``dimension''
changes with scale) is known in the fractal literature.
In principle, the concept of lacunarity should capture quantitative
aspects related to the distribution of magnitudes of holes (``empty'' spaces)
in a fractal structure. Mandelbrot pointed out that there is no unique
all-encompassing way to formally define a measure of lacunarity, and proposed
to characterize texture properties of fractals using the behavior of their cover
functions. In particular, the prefactor oscillations of a Minkowski-Bouligand
cover of a fractal, can be used to describe shell lacunarity. However,
save for some particular classes of mathematical fractals (e.g., Theiler
1988; Mandelbrot 1995), the properties of cover functions and their prefactors
are poorly understood and a systematic approach to their study is lacking.
Moreover, some cover functions may even be nondifferentiable and the presence of
high lacunarity, has the effect of degrading the convergence properties of data
analysis algorithms used to assert fractality and extract scaling exponents.
The aim of this note is to point out that the use of the mathematical Theory of
Regular Variation (in the sense of Karamata) (RVT) and its extensions
(de Haan theory) (Bingham et al. 1987), provides a formal framework to study
more systematically the properties of cover function prefactors for fractal-like
structures and thus, of fractal texture, including lacunarity. Some of the
benefits of the RVT based approach are a) more precise characterizations of a
variety of morphological features of fractal-like structures, not captured by
fractal dimension, in particular, a taxonomy of fractal-like structures based on
the ``roughness" of their cover functions, b) means to quantify differences among
fractals with the same fractal dimensions, in particular, a rigorous approach to
shell lacunarity, c) bounds on rates of convergence for some basic algorithms
used to evaluate fractal dimensions and other scaling exponents, and a base to
develop novel algorithms for this purpose, and d) means to detect and characterize
scale dependence using ``fine'' properties of cover function. The texture
characterization methodology based on regular variation can be used for both,
mono- and multi-fractals, as well as for deterministic and random
fractals.
Below, a very brief overview of the main point of the RVT based approach
is stated. The formal details and examples, including some astrophysical
applications regarding the above mentioned points, will be presented in an
extended version of this note (Stern 1997, in preparation).
Let 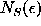 be the smallest number of balls of the same diameter
be the smallest number of balls of the same diameter
 , needed to cover a fractal set S. Then
, needed to cover a fractal set S. Then 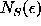 is
a cover function which provides the box dimension of S as
is
a cover function which provides the box dimension of S as
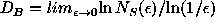 ,
if the limit exists. The box dimension is the most common form of ``fractal
dimension'' encountered in applications. Denote,
,
if the limit exists. The box dimension is the most common form of ``fractal
dimension'' encountered in applications. Denote, 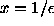 ; x is a
convenient scale variable for the RVT approach. Asymptotically, the power-law
form of this cover function, is,
; x is a
convenient scale variable for the RVT approach. Asymptotically, the power-law
form of this cover function, is, 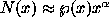 , where
, where
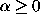 . In general, it is assumed in literature that the various
cover functions used to extract scaling exponents are power-law-like
functions. The main reason why RVT provides a natural framework to study cover
functions is that it is a general mathematical theory focusing on asymptotic
properties of functions under rescaling transformations of the argument.
In particular, RVT provides a general theory of power-law-like behavior,
including ``correction factors'' and other fine properties of such functions.
. In general, it is assumed in literature that the various
cover functions used to extract scaling exponents are power-law-like
functions. The main reason why RVT provides a natural framework to study cover
functions is that it is a general mathematical theory focusing on asymptotic
properties of functions under rescaling transformations of the argument.
In particular, RVT provides a general theory of power-law-like behavior,
including ``correction factors'' and other fine properties of such functions.
The function 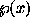 has a slower growth than x and is called a
prefactor function. For simple, self-similar fractals the prefactors,
has a slower growth than x and is called a
prefactor function. For simple, self-similar fractals the prefactors,
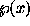 , are periodic functions in
, are periodic functions in 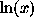 . However, various other forms of
prefactor behavior reflecting textural properties of the fractal structure, are
possible. This wide spectrum of behaviors can be understood and classified
using RVT.
. However, various other forms of
prefactor behavior reflecting textural properties of the fractal structure, are
possible. This wide spectrum of behaviors can be understood and classified
using RVT.
Let 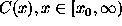 be a generic cover function. The most basic
type of behavior of
be a generic cover function. The most basic
type of behavior of 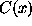 in RVT is known as regular variation.
in RVT is known as regular variation. 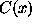 is regularly varying at infinity (RV) if
is regularly varying at infinity (RV) if
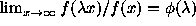 ,
where
,
where 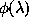 depends only on
depends only on 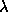 , and has the form
, and has the form
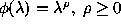 , for any
, for any 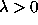 .
.
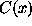 is slowly varying (SV) if
is slowly varying (SV) if 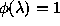 , i.e.,
, i.e.,
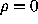 . A slowly varying function cannot grow or decrease ``as fast'' as a
power of x. The exponent
. A slowly varying function cannot grow or decrease ``as fast'' as a
power of x. The exponent 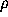 is called in RVT, the regular variation
index of
is called in RVT, the regular variation
index of 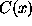 .
.
The ``simplest'' fractals, from RVT point of view, have a cover, 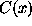 , which
is RV. Such fractals are called here soft. For soft fractals
, which
is RV. Such fractals are called here soft. For soft fractals 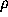 coincides with the fractal dimension. Soft fractals are important for applications,
since they have ``low lacunarity'' in the sense that the prefactors are SV functions,
and many random fractals of practical interest are likely to be soft, because
``randomness'' may wash out to some extent strong prefactor oscillations.
For soft fractals, a detailed formalism for convergence rates of algorithms for
scaling exponents can be provided. The study of fractals with stronger prefactor
oscillations than allowed by RV, needs the use of the more involved concepts of
extended regular variation and O-regular variation (see Bingham
et al. 1987; Stern 1997, in preparation).
coincides with the fractal dimension. Soft fractals are important for applications,
since they have ``low lacunarity'' in the sense that the prefactors are SV functions,
and many random fractals of practical interest are likely to be soft, because
``randomness'' may wash out to some extent strong prefactor oscillations.
For soft fractals, a detailed formalism for convergence rates of algorithms for
scaling exponents can be provided. The study of fractals with stronger prefactor
oscillations than allowed by RV, needs the use of the more involved concepts of
extended regular variation and O-regular variation (see Bingham
et al. 1987; Stern 1997, in preparation).
The above sketched RVT approach can help to better understand the properties
of solid packings of finite regions of 3-D space. The possibility of such a
modeling approach to galaxy distributions was suggested by Mandelbrot in his
celebrated book (Mandelbrot 1983). Consider, for example, the cover of such a
region with nonoverlapping, tangent spheres of different radii (``cosmic
voids''). The residual set remaining after removing these spheres is a
geometrical construct which is known to be a geometrical multifractal, if the
packing is ``solid,'' that is, if the Lebesque measure of the residual set is zero.
If the covering spheres are generated deterministically and recursively, the
packing is ``apollonian'' (suggested by Apollon of Perga, 200 BC). Stochastic
processes leading to solid random packings of this kind are also possible.
The infinite sets of tangency points of the spheres in these constructions
form multifractal point sets, providing nontrivial examples of fractal
``hierarchical clustering'' geometries, potentially relevant to distributions
of galaxy counts. These sets can also serve as support for multifractal mass
distribution models as well as, a class of generic toy models alternative to
more familiar ``beta''-type multifractal models common in the galaxy count
distributions literature. A visual examination of such tangency point sets
suggests that some clustering patterns in such point distributions can mimic,
crudely, structures like ``walls,'' ``filaments,'' and ``voids'' on ``all scales,''
etc. Few generic results exist in the mathematical literature regarding such
point sets. For a 3-D apollonian covering with spheres, a crude estimate of the
fractal dimension exists (Boyd 1973 gives the value of 2.4). An RVT based
approach was undertaken to refine this estimate and investigate the lacunarity
of such models, using the properties of a ranked series of radii of the 3-D
covering spheres. The formal details and results will be reported elsewhere.
The specific texture of a fractal cannot be ignored in the study
of fractal-like structures of interest for astrophysics. Textural
features carry information about the generating dynamics of a fractal.
Information about texture, contained in prefactors of cover functions can be
analyzed if the sampling of the structure in ``resolution space'' is not too
sparse. RVT provides a useful formal framework to understand the variety of
possible prefactor behaviors and their impact on convergence rates of
algorithms for scaling exponents.
A class of multifractal structures based on apollonian-like solid packings of
space with spheres may provide an interesting modeling approach to some scaling
properties of the large scale distribution of matter. The RVT based methodology,
provides some novel ways to study such structures in more detail.
References:
Bingham, N. H., Goldie, C. M., & Teugels, J. L. 1987, Regular
Variation (Cambridge: Cambridge Univ. Press)
Borgani, S. 1995, Phys. Reports, 251, 1
Boyd, D. 1973, Mathematics of Computation, 27, 369
Labini, F. S., Gabrielli, A., Montuori, M.,
& Pietronero, L. 1996, Physica A, 226, 195
Mandelbrot, B. B. 1983, The Fractal Geometry of Nature (San
Francisco: W. H. Freeman)
Mandelbrot, B. B. 1995, in Progress in Probability, Vol. 37,
Fractal Geometry and Stochastics, ed. C. Bandt, S. Graf, & M. Zahle (Basel: Birkhauser)
Peebles, P. J. E. 1993, Principles of Physical Cosmology
(Princeton: Princeton Univ. Press)
Theiler, J. 1988, Thesis, California Institute of Technology
© Copyright 1997 Astronomical Society of the Pacific,
390 Ashton Avenue, San Francisco, California 94112, USA
Next: Using Massively Parallel Processing of a NLTE Spectrum Synthetic Code and an Automated Comparison with Observations to Determine the Properties of Type Ia Supernovae from their Late Time Spectra.
Previous: Numerical Simulations of Plasmas and Their Spectra
Up: Modeling
Table of Contents - Index - PS reprint
payne@stsci.edu
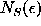 be the smallest number of balls of the same diameter
be the smallest number of balls of the same diameter
 , needed to cover a fractal set S. Then
, needed to cover a fractal set S. Then 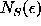 is
a cover function which provides the box dimension of S as
is
a cover function which provides the box dimension of S as
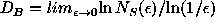 ,
if the limit exists. The box dimension is the most common form of ``fractal
dimension'' encountered in applications. Denote,
,
if the limit exists. The box dimension is the most common form of ``fractal
dimension'' encountered in applications. Denote, 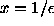 ; x is a
convenient scale variable for the RVT approach. Asymptotically, the power-law
form of this cover function, is,
; x is a
convenient scale variable for the RVT approach. Asymptotically, the power-law
form of this cover function, is, 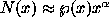 , where
, where
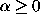 . In general, it is assumed in literature that the various
cover functions used to extract scaling exponents are power-law-like
functions. The main reason why RVT provides a natural framework to study cover
functions is that it is a general mathematical theory focusing on asymptotic
properties of functions under rescaling transformations of the argument.
In particular, RVT provides a general theory of power-law-like behavior,
including ``correction factors'' and other fine properties of such functions.
. In general, it is assumed in literature that the various
cover functions used to extract scaling exponents are power-law-like
functions. The main reason why RVT provides a natural framework to study cover
functions is that it is a general mathematical theory focusing on asymptotic
properties of functions under rescaling transformations of the argument.
In particular, RVT provides a general theory of power-law-like behavior,
including ``correction factors'' and other fine properties of such functions.
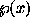 has a slower growth than x and is called a
prefactor function. For simple, self-similar fractals the prefactors,
has a slower growth than x and is called a
prefactor function. For simple, self-similar fractals the prefactors,
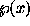 , are periodic functions in
, are periodic functions in 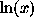 . However, various other forms of
prefactor behavior reflecting textural properties of the fractal structure, are
possible. This wide spectrum of behaviors can be understood and classified
using RVT.
. However, various other forms of
prefactor behavior reflecting textural properties of the fractal structure, are
possible. This wide spectrum of behaviors can be understood and classified
using RVT.
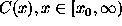 be a generic cover function. The most basic
type of behavior of
be a generic cover function. The most basic
type of behavior of 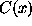 in RVT is known as regular variation.
in RVT is known as regular variation. 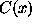 is regularly varying at infinity (RV) if
is regularly varying at infinity (RV) if
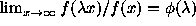 ,
where
,
where 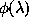 depends only on
depends only on 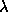 , and has the form
, and has the form
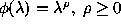 , for any
, for any 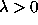 .
.
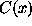 is slowly varying (SV) if
is slowly varying (SV) if 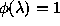 , i.e.,
, i.e.,
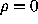 . A slowly varying function cannot grow or decrease ``as fast'' as a
power of x. The exponent
. A slowly varying function cannot grow or decrease ``as fast'' as a
power of x. The exponent 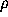 is called in RVT, the regular variation
index of
is called in RVT, the regular variation
index of 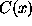 .
.
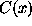 , which
is RV. Such fractals are called here soft. For soft fractals
, which
is RV. Such fractals are called here soft. For soft fractals 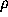 coincides with the fractal dimension. Soft fractals are important for applications,
since they have ``low lacunarity'' in the sense that the prefactors are SV functions,
and many random fractals of practical interest are likely to be soft, because
``randomness'' may wash out to some extent strong prefactor oscillations.
For soft fractals, a detailed formalism for convergence rates of algorithms for
scaling exponents can be provided. The study of fractals with stronger prefactor
oscillations than allowed by RV, needs the use of the more involved concepts of
extended regular variation and O-regular variation (see Bingham
et al. 1987; Stern 1997, in preparation).
coincides with the fractal dimension. Soft fractals are important for applications,
since they have ``low lacunarity'' in the sense that the prefactors are SV functions,
and many random fractals of practical interest are likely to be soft, because
``randomness'' may wash out to some extent strong prefactor oscillations.
For soft fractals, a detailed formalism for convergence rates of algorithms for
scaling exponents can be provided. The study of fractals with stronger prefactor
oscillations than allowed by RV, needs the use of the more involved concepts of
extended regular variation and O-regular variation (see Bingham
et al. 1987; Stern 1997, in preparation).