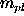in the
corotating coordinate system take the form:
Next: Imaging by an Optimizing Method
Previous: The Time Interferometer: Synthesis of the Correlation Function
Up: Algorithms
Table of Contents - Index - PS reprint
Tanya Taidakova
Crimean Astrophysical Observatory, Simeiz, 334242, Ukraine
In the last few years there has been great interest in the numerical study of long term evolution of bodies of the Solar system. As the integration time increases, the numerical results become more contaminated by various errors. The most serious error is the accumulation of the discretization (truncation) error due to a finite stepsize (or the replacement of continuous differential equations by finite difference equations). The conventional integrators such as Runge-Kutta, multi-step and Taylor methods, generate linear secular errors in orbital energy and angular momentum. This means that the semi-major axis and the eccentricity change linearly with time and the linear secular error in the semi-major axis produces a quadratic secular error in the planetary longitude. A new symplectic integrator produces no secular truncation errors in the actions of a Hamiltonian system.
In this paper we briefly discuss an implicit numerical
integrator. The discretization errors in the energy, the
semi-major axis, and the eccentricity by the implicit
second-order integrator show only periodic changes. The
truncation error in the argument of pericenter grows linearly
in time.
The equations of motion of a particle in the gravitational
field of the Sun and the planet with mass 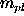in the
corotating coordinate system take the form:
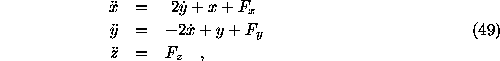
where:
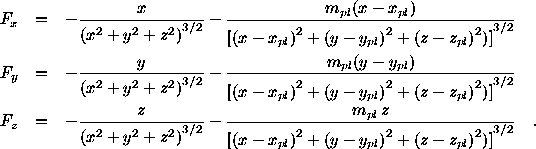
Here the total mass of the Sun and the planet is taken as the unit of
mass, and the distance between the planet and the Sun is taken as
the unit of length. The unit of time is chosen in such a way that
the angular velocity of orbital motion of the planet is equal to
unity, and, hence, its orbital period is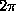 
.
Let 
, 
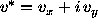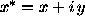, and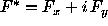 
. We
obtain rather than (1):
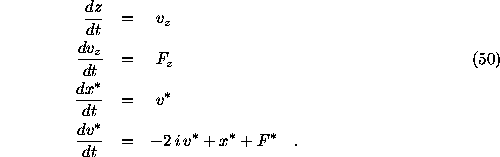
We may solve the equation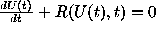 
with initial conditions 
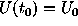by the implicit
second-order integrator described in Potter (1973):
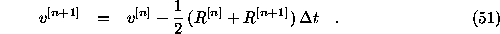
In our equations (2), R is a function of x,y,z. We will
calculate this function R in space-time points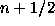 
.
From (2) by the use of Eq. (3) we derive the equations for new
integrator (Taidakova 1990, 1995):
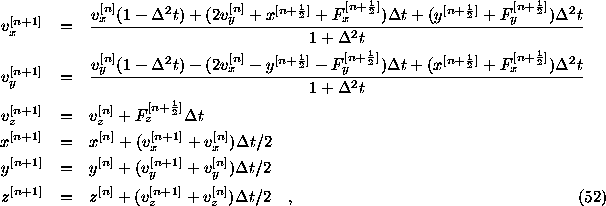
where: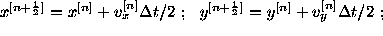
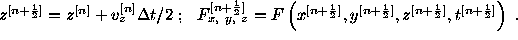
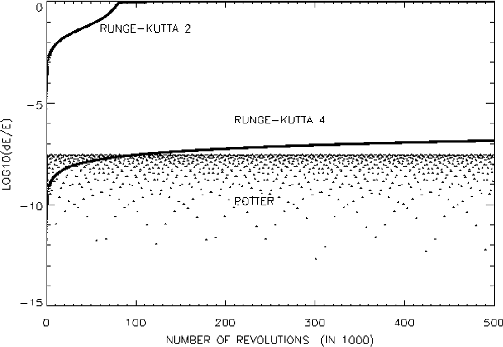
Figure: Numerical errors in the energy with second order Runge-Kutta,
fourth order Runge-Kutta and second order Potter integrator.
Original PostScript figure (1.70MB).
We tested this method for several astronomical
systems (Taidakova 1995). In order to see the properties of
the implicit integrator, we first choose the 2-body problem.
Figure 1 shows the numerical errors in the energy
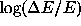in the numerical integrations of the motion
of the particle in circular orbit around the Sun with
different integrators. Figure 2 shows the errors in the parameter
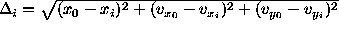, where i is the number of revolutions, x
is the coordinate 
, and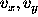 
are the velocities in the
numerical integration of the orbital motion of asteroid in
the 1:1 Jupiter resonance during 200 million steps. The computer
time with the implicit second-order integrator is about 1.52-1.94
times faster than that with second-order Runge-Kutta integrator.
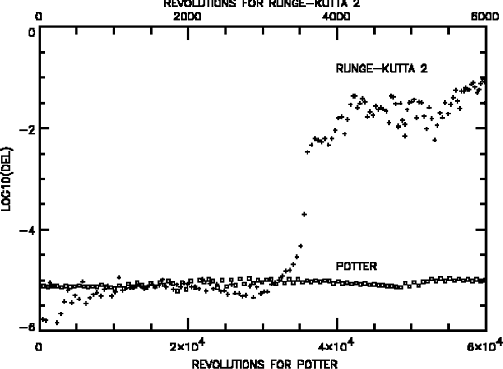
Figure: Numerical errors in the parameter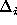 
with second order Runge-Kutta method and second order Potter integrator.
Original PostScript figure (1.82MB).
The calculation were carried out in a PC with DX4/100.
The author thanks the Local Organizing Committee and U.S. Civilian Research & Development Foundation (Grant # 96023) for support.
Potter, D. 1973, Computational Physics (New York: Wiley)
Taidakova, T. 1990, Nauch.Inform.Astrosoveta Akademii Nauk SSSR (Riga: Zinatne), 68, 72
Taidakova, T. 1995, Ph.D. Thesis, Moscow State University
Next: Imaging by an Optimizing Method
Previous: The Time Interferometer: Synthesis of the Correlation Function
Up: Algorithms
Table of Contents - Index - PS reprint