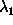 and
and 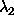 can be considered as new
parameters instead of the widely used system of four interdependent
parameters (
can be considered as new
parameters instead of the widely used system of four interdependent
parameters (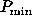 ,
, 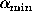 ,
, 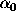 , and h), and are more
suitable for further analysis (Vasilyev 1996).
, and h), and are more
suitable for further analysis (Vasilyev 1996).
Next: Unified Survey of Fourier Synthesis Methodologies
Previous: Heuristic Estimates of Weighted Binomial Statistics for Use in Detecting Rare Point Source Transients
Up: Algorithms
Table of Contents - Index - PS reprint
S. Vasilyev
SOLERC, P.O. Box 59, Kharkiv, 310052, Ukraine
In recent years the spectrum of observed astronomical data can be characterized as greatly varied. In particular, this can be explained by the rapid growth in the number of objects studied and the appearance of new data types due to the progress in space-based observations. In this instance, the problem of initial description and classification of newly-observed data becomes most urgent, especially if there is a lack of preliminary observational material and theoretical expectations.
The literature developing methods to treat statistical data sequences is ample but many studies are based on the face of data images and have difficulties determining the minimum set of independent parameters appropriate for further analysis. The well-known principal component method of the multivariate statistical data treatment can be extended in order to obtain a tool for determination of the independent parameters applicable for reliable data representation and further comprehensive analysis.
The distinction of the approach consists in the direct use of the observed data records as input parameters in composing the initial and covariance matrices involved in further analysis. Each of n observational dependencies forms a row in the initial matrix and is represented by a vector in m-dimensional space in accordance with the number of observed dependencies and the number of points on each curve, respectively. These n vectors determine the dimension of the covariance matrix and thus the number of its eigenvectors and eigenvalues. The eigenvectors are orthogonal and, consequently, each row of the covariance matrix, as well as that of the initial one can be only expressed by their linear combination. It is advisable to normalize the eigenvectors by dividing them by their lengths, which are equal to the square roots of the corresponding eigenvalues. This puts the eigenvectors on the same scale.
Finding the eigenvalues often makes it possible to represent the initial matrix with needed accuracy by taking a linear combination of a relatively small number of principal components corresponding to the largest eigenvalues and so bearing most of the information on the data (Genderon & Goddard 1966). The other principal components are usually responsible for the random noise in observations and can be neglected from consideration (Lorge & Morrison 1938). The quality of data representation can be controlled with a test matrix composed of linear combinations of the principal components multiplied by the corresponding eigenvalues.
Generally, analytical functions for the selected principal components can
be found by fitting, and we obtain the data being analytically
represented in addition. In this case, all of the initial dependencies can be
easily calculated as linear combinations of the functions, which
are presumably described by a minimum parameter set. We have developed an
interactive computer package which can automatically describe some kinds of data by
principal components. The software also
performs the preliminary data fitting on the measurements, which are not
uniformly tabulated observational records. The procedure
of finding the largest eigenvalues and corresponding eigenvectors, or
principal components, is based on the algorithm presented
in Simonds (1963). The approach has been successfully applied to describe
all of the variety of the asteroid polarization phase dependencies
(Vasilyev 1994) and tested for some other types of data.
We have found two principal components which are adequate to represent any
polarization curve belonging to the analyzed assemblage and even for data
not involved in the initial analysis. The corresponding
eigenvalues 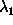 and
and 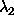 can be considered as new
parameters instead of the widely used system of four interdependent
parameters (
can be considered as new
parameters instead of the widely used system of four interdependent
parameters (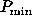 ,
, 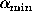 ,
, 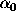 , and h), and are more
suitable for further analysis (Vasilyev 1996).
, and h), and are more
suitable for further analysis (Vasilyev 1996).
Expressions obtained for the principal components can be used to describe new data and gappy observational dependencies. In the case of asteroids, the method allows the synthesis of the polarization curves using only three observations and shows a better fit to the data compared to other fitting techniques tried. The power of this method is its intrinsic ability to find the principal peculiarities appropriate to all the data under study. It can be efficiently used for restoring truncated data records and rationally planning further observations.
Although the principal component method itself does not imply knowledge of the physical nature of the analyzed data, it often allows connection of the principal components with the physical parameters of the objects. In particular, we have found that both of the principal components of the family of asteroid polarimetric phase curves have physical meanings and the fit correlations were determined.
Additional useful possibilities give the correlative diagrams of the largest eigenvalues corresponding to the first principal components. These diagrams do not exhibit any mutual correlation between the eigenvalues, of course, as it is required by the technique. However, they may reveal the differences in properties among the analyzed data and can be successfully used for independent classification of the studied objects (Tholen 1984; Vasilyev 1996).
As the number of the principal components and corresponding eigenvalues used for the data representation is usually much smaller than that of the observed dependencies, we obtain an alternative tool for compact data storage. The problem of finding the balance between the required accuracy of the data restoration and the needed compression ratio is the subject of a separate study. Our preliminary results show that the use of the principal component technique can reduce the data volume by up to several times (Vasilyev 1995). In the instance of the asteroid polarimetric data the compression ratio was increased to a factor of five, while the differences between the initial and restored data did not exceed the errors in observations. Furthermore, as the principal components keep the data structure, this ratio can be increased by the subsequent application of any other archiving software.
The technique based on the principal component analysis of the data records may serve as a powerful tool for the initial statistical data treatment allowing data inter/extrapolation, analytical representation, classification, and compact storage. Among the advantages of the technique are the stability of the obtained eigenvectors when adding new data and the minimizing the rms errors in data representation. It is important that the application of this approach does not require any a priori assumption, either about the objects or about the physical mechanisms under study. In order to make possible such a multipurpose application of the technique for some types of the newly observed data in the automatic mode we are currently developing an integrated program package PCMAD (Principal Component Method for Astronomical Data) including the most of the described features. It should be noted that the method has no special requirements of computer performance except during the first stage of its application when the matrix operations are performed.
Genderon, R. G., & Goddard, M. G. 1966, Photogr. Sci. Eng, 10, 77
Lorge, J., & Morrison N. 1938, Science, 87, 491
Simonds, J. L. 1963, J. Opt. Soc. America, 53, 968
Tholen, D. J. 1984, Ph.D. Thesis, Univ. of Arizona
Vasilyev, S. V. 1994, BAAS, 26, 1173
Vasilyev, S. V. 1995, Vistas in Astronomy, 39, 275
Vasilyev, S. V. 1996, Ph.D. Thesis, Kharkiv St. Univ., Ukraine
Next: Unified Survey of Fourier Synthesis Methodologies
Previous: Heuristic Estimates of Weighted Binomial Statistics for Use in Detecting Rare Point Source Transients
Up: Algorithms
Table of Contents - Index - PS reprint