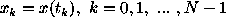with zero mean obtained at arbitrary times 
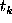, we can set up the model
Next: The Time Interferometer: Synthesis of the Correlation Function
Previous: Determination of Variable Time Delay in Uneven Data Sets
Up: Algorithms
Table of Contents - Index - PS reprint
V. V. Vityazev
Astronomy Department, St. Petersburg University, Bibliotechnaya pl.2,
Petrodvorets, St. Petersburg, 198904, Russia.
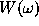corresponding to the
distribution of time points. The main results are: a) all the
estimators evaluated at frequency 
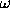are identical if
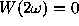; b) the Schuster periodogram differs from the LS-spectra
at the frequencies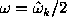 
, where
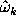are the
frequencies at which the spectral window has large side peaks due to
irregular distribution of time points. Two examples for
situations typical in astronomy illustrate these conclusions.
In various branches of astronomy, we face the problem of finding periodicities hidden in observations. If the data are regularly spaced in time, the Schuster periodogram is the basic tool for evaluating the power spectra (Marple 1987; Terebizh 1992). Unfortunately, astronomical observations are irregular for various reasons: day-time changes, weather conditions, positions of the object under observations, etc. Present day theory and practice of the spectral analysis of unequally spaced time series are based on two approaches. The first one employs the Schuster periodogram (Deeming 1975; Roberts et al. 1987). The second one uses the procedure of the least squares fitting of a sinusoid to the data (Barning 1962; Lomb 1976; Scargle 1982) with resulting estimators known as the LS-spectra. The most valuable feature of the LS-spectra is well defined statistical behavior. At the same time, the LS-spectra lose very important properties: description in terms of the spectral window, connection with the correlation function, etc. On the other hand, the Schuster periodogram of a gapped time series satisfies all the fundamental relations of the classical spectral analysis, but its statistical properties are complicated as compared to the case of regular data. It is worth mentioning that despite different theoretical foundations, the Schuster periodogram and the LS-spectra frequently turn out to be almost identical. This similarity requires an explanation, and we are trying to find situations when the Schuster periodogram and the LS-spectra are very close to each other or differ greatly. The ultimate goal of this study is to clarify the properties of various techniques which are used to derive the periodicities from the unequally distributed data.
For a set of N observations
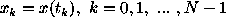with zero mean obtained at arbitrary times 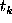, we can set up the model
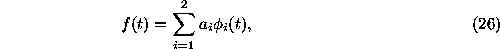
where
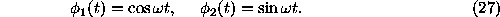
Using the following notation
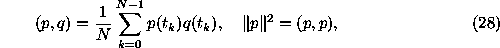
the ``classical'' estimator of the power spectrum (the Schuster periodogram) can be written in the form
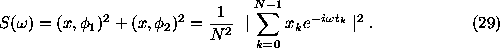
If the signal contains a sine function of
frequency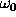 
, then the product 
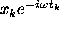makes a
large contribution to S provided that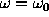 
. In other
words, the Schuster periodogram, to the limit of normalizing factor,
is a square of the correlation coefficient between the data and a
harmonic function.
The alternative estimator of the power spectrum based on the least squares fitting of the sine function to the data was proposed by Lomb (1976) and Scargle (1982). Their approach is based on the introduction of the new time points
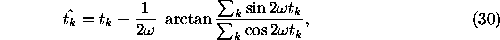
where the time shift provides the orthogonality of the functions
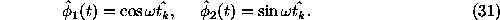
Under this assumption the LS-spectrum looks as follows:
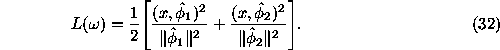
Thus we see that the Schuster periodogram differs from the LS-spectra by definition.
The intercomparison between the Schuster periodogram and the LS-spectrum is given by the following
Theorem. At the set of frequencies that satisfy equation
where the spectral windowis
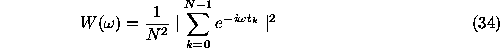
the Schuster periodogram and the LS-spectra are identical.
In this section we consider two typical distributions of points for which the frequencies that satisfy Eq. (8) do exist.
Astronomical observations are often performed with periodic gaps.
Ground-based observations are interrupted by day-night alternation;
the observations from a space vehicle are usually stopped when the satellite
enters the radiation belts. To model the situations we suppose that,
in the set of observations with a constant interval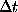 
, one
has n
successive observations and p successive missing points, and the
group of n+p points is repeated m times, so the period of
gaps is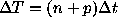 
.
In the previous paper
(Vityazev 1994) it was shown that in this case the spectral window
looks as follows
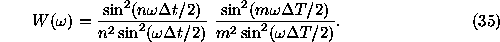
It is easy to find that the frequencies
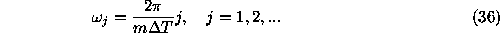
satisfy Eq. (8), provided that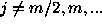 
if m is even and
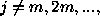if m is odd.
Considered here is a situation where two sets of observations (each one
consisting of n successive points) are separated by p missing points
forming the gap. As earlier, all the points are supposed to be regularly
spaced over the time interval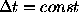 
. Now, for the spectral
window we have (Vityazev 1994)
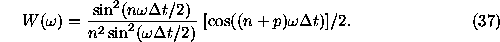
It is not difficult to show that the frequencies
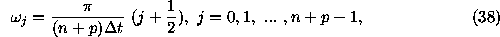
satisfy the condition of Eq. (8).
The LS-spectra gained popularity due to the fact that they retain the exponential distribution of their accounts when the time series is assumed to be white noise. Now we see that at frequencies that satisfy Eq. (8) the Schuster periodogram retains the exponential distribution too.
The Schuster periodogram differs from the LS-spectra only at the
frequencies that satisfy the condition 1-W(2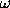
) 
1. It
means that the discrepancies between the Schuster periodogram and the
LS-spectra are large when the time series contain a harmonic of the
frequency, the double value of which coincides with the frequency at
which the spectral window has a large side peak. In the case of
periodical gaps it happens when the period of a signal hidden
in the data is one half the period of the gaps.
In this situation (Vityazev 1997a), the spectral estimation faces
unrealistic intensities of
the spectral peaks and the strong dependence
of the heights of peaks on the phase of the signal. It is very
important to emphasize that these problems come not from the choice of
the tool to evaluate the power spectrum; they originate from mixing
two sources of the
periodicities: one is the physical process that we observe and
another one is a periodical interruption of observations.
In astronomy, the rotation and revolution of the Earth impose diurnal
and annual cycles on the Earth-based observations. The periods hidden
in observations of the Sun, stars, quasars, etc., are hardly connected
physically with the periods specific to the Earth. For these
observations, the probability of mixing
periodicities is negligible. On the contrary, if
we study the Earth from the Earth (such is the case with
astrometric observations of the Earth's rotation parameters), then the
semi-annual period in the Earth's rotation interferes with the
annual gaps in observations.
For further details the reader is referred to Vityazev (1997a, 1997b).
Barning, F. J. M. 1962, B.A.N., 17, N1, 22
Deeming, T. J. 1975, Ap&SS, 36, 137
Lomb, N. R. 1976, Ap&SS, 39, 447
Marple, Jr., S. L. 1987, Digital Spectral Analysis with Applications (Englewood Cliffs, NJ: Prentice-Hall)
Roberts, D. H., Lehar, J., & Dreher, J. W. 1987, AJ, 93, 968
Scargle, J. D. 1982, ApJ, 263, 835
Terebish, V. Yu. 1992. Time Series Analysis in Astrophysics (Moscow: Nauka)
Vityazev, V. V. 1994, Astron. and Astrophys. Tr., 5, 177
Vityazev, V. V. 1997a, A&A, in press
Vityazev, V. V. 1997b, A&A, in press
Next: The Time Interferometer: Synthesis of the Correlation Function
Previous: Determination of Variable Time Delay in Uneven Data Sets
Up: Algorithms
Table of Contents - Index - PS reprint