The relativity principle states that the laws of physics are the same in all rigid inertial frames, so observers in different inertial frames should be able to compare measurements after suitable coordinate transformations.

Figure C.1 shows the inertial coordinate system $S$ and the “primed” system $S^{\prime }$ moving with a constant velocity $v$ along their common $x$-axis. The planes $y=0$ and $z=0$ always coincide with the planes $y^{\prime }=0$ and $z^{\prime }=0$, and clocks in both frames were synchronized by setting $t=t^{\prime }=0$ at the instant when $x=x^{\prime }$.

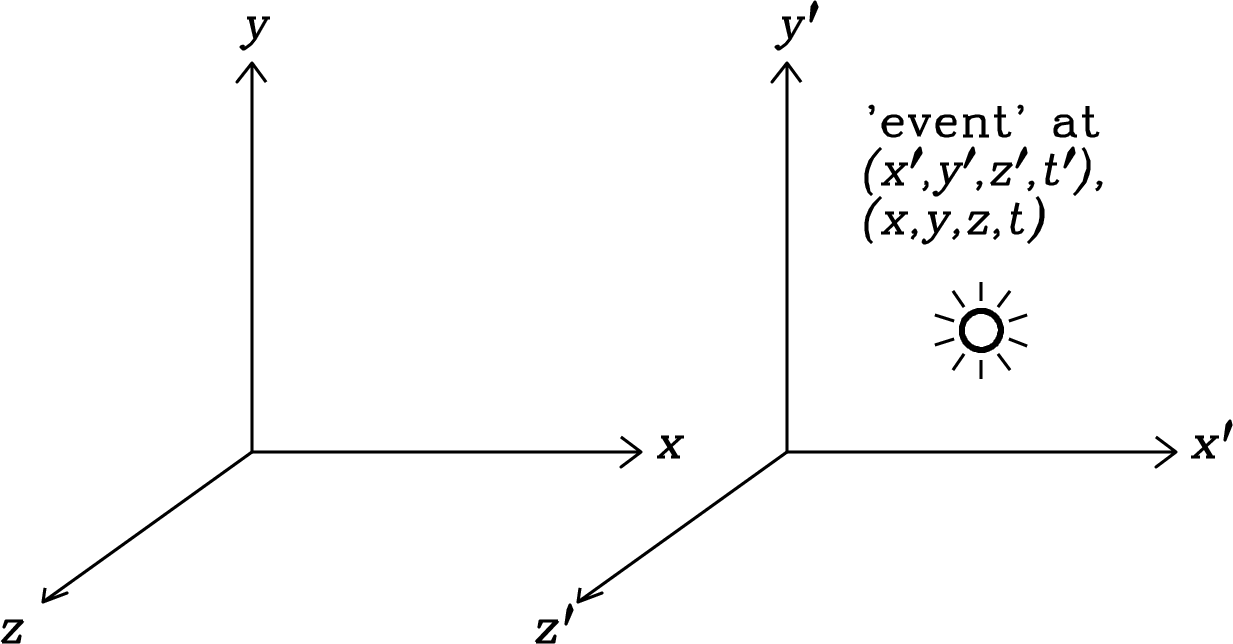
An event is an observable confined to one point in space and time, such as a camera flash firing. The event coordinates in $S$ and $S^{\prime }$ are $(x,y,z,t)$ and $(x^{\prime },y^{\prime },z^{\prime },t^{\prime })$, respectively.

According to “everyday” Galilean relativity, the event coordinates in $S$ are related to those in $S^{\prime }$ by the Galilean transform

	$x=x^{\prime }+v{t}^{\prime },$	$\mathrm{\hspace{1em}\hspace{1em}}y=y^{\prime },z=z^{\prime },t=t^{\prime },$		(C.1)
	$x^{\prime }=x-vt,$	$\mathrm{\hspace{1em}\hspace{1em}}{y}^{\prime }=y,z^{\prime }=z,t^{\prime }=t.$		(C.2)

However, everyday experience with slowly moving objects cannot be extrapolated to speeds approaching the vacuum speed of light $c$. Everyday experience suggests that $t=t^{\prime }$ in all inertial frames, so Isaac Newton believed in “absolute, true, and mathematical time, in and of itself and of its own nature, without reference to anything external.” If $t=t^{\prime }$ and $x=x^{\prime }+v{t}^{\prime }$, parallel velocities simply add. The speed of a photon emitted in the $+x^{\prime }$-direction by a flash at rest in the $S^{\prime }$ system will be seen by an observer in the $S$ frame as

$$c_x=\frac{dx}{dt}=\frac{d(x^{\prime }+v{t}^{\prime })}{d{t}^{\prime }}=\frac{d{x}^{\prime }}{d{t}^{\prime }}+v=c_x^{\prime }+v.$$

(C.3)

Thus Galilean relativity is inconsistent with both observation and Maxwell’s equations, which correctly predict that the speed of light in a vacuum is the same for all observers in all inertial frames ($c_x=c_x^{\prime }$), regardless of their relative velocities $v$. Apparently time is not absolute, and identical clocks in the $S$ and $S^{\prime }$ frames do not run at the same rates: $t\ne t^{\prime }$.

The Lorentz transform is the only coordinate transform consistent with both relativity and the existence of some still-unspecified invariant speed $c$ (for example, the vacuum speed of light, or even $\mathrm{\infty }$). The assumption that there exists some invariant speed is actually weaker than assuming $t=t^{\prime }$ because it turns out that $c=\mathrm{\infty }$ reduces the Lorentz transform to the Galilean transform.

The Lorentz transform can be derived with two additional assumptions (see Rindler [91, p. 39] or Rindler [92, p. 12]):

1. 1.

   space is homogeneous, and

2. 2.

   space is isotropic.

These assumptions say that the laws of physics are invariant under translation and rotation of the coordinate frames.

Homogeneity implies that any transformation from one inertial frame to another must be linear; that is, $y^{\prime }=Ay+B$ where $A$ and $B$ are constants. Adding nonlinear terms (e.g., $y^{\prime }=Ay+B+C{y}^2$) would cause the transform itself to vary under coordinate translations, so $C=0$ in a homogeneous space. Because the coordinate frames were chosen such that $y=0$ when $y^{\prime }=0$, linearity also requires that $B=0$, leaving $y^{\prime }=Ay$, where $A$ is a still-unspecified scale factor.

Isotropy implies that the observers in both frames agree on their relative speed $|v|$ because a 180${}^{\circ }$ coordinate rotation exchanges the roles of the two frames. That rotation should have no effect if space is isotropic, so $y^{\prime }=Ay$ implies $y=A^{\prime }{y}^{\prime }$ and only $A=A^{\prime }=\pm 1$ is consistent with isotropy. The negative solution $A=-1$ can be rejected because it implies $y=-y^{\prime }$ even when $v=0$. These arguments can also be applied to $z$ and $z^{\prime }$, so the Lorentz transform for the $y$ and $z$ coordinates is

$$y=y^{\prime },z=z^{\prime },$$

(C.4)

in agreement with the Galilean transform (Equation C.1).

For the $x$-coordinate, linearity requires

$$x={\gamma }^{\prime }(x^{\prime }+v{t}^{\prime }),x^{\prime }=\gamma (x-vt),$$

(C.5)

where ${\gamma }^{\prime }$ and $\gamma$ are still-unspecified constant scale factors. In Galilean relativity, $\gamma ={\gamma }^{\prime }=1$.

Invoking isotropy and reversing the directions of $S$ and $S^{\prime }$ gives

$$x={\gamma }^{\prime }(x^{\prime }-v{t}^{\prime }),x^{\prime }=\gamma (x+vt)$$

(C.6)

and reversing the roles of the two frames gives

$$x=\gamma (x^{\prime }-v{t}^{\prime }),x^{\prime }={\gamma }^{\prime }(x+vt)\text{.}$$

(C.7)

Equations C.6 and C.7 together imply $\gamma ={\gamma }^{\prime }$; that is, the observers in $S$ and $S^{\prime }$ agree on the value of the coordinate scale factor $\gamma$ associated with their relative velocity $v$.

We now make use of the assumption that there is some speed $c$ which is the same in all inertial frames. Maxwell’s equations and experiment both show that $c$ is the speed of light in a vacuum, but for this argument, the invariant speed might be any speed, even $c=\mathrm{\infty }$, in which limit the Lorentz transform turns out to be identical to the Galilean transform. Then $x=ct$ implies $x^{\prime }=c{t}^{\prime }$ and Equation C.5 implies

$$ct=\gamma t^{\prime }(c+v),c{t}^{\prime }=\gamma t(c-v).$$

(C.8)

The product

$$c^{2}t{t}^{\prime }={\gamma }^{2}t{t}^{\prime }(c+v)(c-v)$$

(C.9)

of these two equations can be solved for the Lorentz factor:

$$\boxed{\gamma ={(1-\frac{v^2}{c^2})}^{-1/2}={(1-{\beta }^2)}^{-1/2},}$$

(C.10)

where the dimensionless velocity $\beta$ is defined as

$$\boxed{\beta \equiv \frac{v}{c}.}$$

(C.11)

Again, the negative solution to Equation C.10 can be rejected as unphysical. Notice that $\gamma \ge 1$ for all possible $\beta \le 1$. The $x$-coordinate Lorentz transform becomes

$$x=\gamma (x^{\prime }+v{t}^{\prime }),x^{\prime }=\gamma (x-vt).$$

(C.12)

Eliminating $x$ or $x^{\prime }$ from this pair of equations yields the Lorentz time transform

$$t=\gamma (t^{\prime }+\beta x^{\prime }/c),t^{\prime }=\gamma (t-\beta x/c).$$

(C.13)

In summary, the Lorentz coordinate transform of special relativity is

$$\boxed{x=\gamma (x^{\prime }+v{t}^{\prime }),y=y^{\prime },z=z^{\prime },t=\gamma (t^{\prime }+\beta x^{\prime }/c),}$$

(C.14)

$$\boxed{x^{\prime }=\gamma (x-vt),y^{\prime }=y,z^{\prime }=z,t^{\prime }=\gamma (t-\beta x/c).}$$

(C.15)

Note that in the limit $\beta \to 0$ ($v\ll c$), the Lorentz transform reduces to the Galilean transform (Equation C.1), as it must to agree with “everyday” observations involving small velocities. Equations C.14 and C.15 also show that the Lorentz transform reduces to the Galilean transform for any finite $v$ in the limit $c\to \mathrm{\infty }$, so the assumption that there exists some invariant velocity is not restrictive.

If $(\mathrm{\Delta }x,\mathrm{\Delta }y,\mathrm{\Delta }z,\mathrm{\Delta }t)$ and $(\mathrm{\Delta }{x}^{\prime },\mathrm{\Delta }{y}^{\prime },\mathrm{\Delta }{z}^{\prime },\mathrm{\Delta }{t}^{\prime })$ are the coordinate differences between two events, the differential Lorentz transform is

$$\boxed{\mathrm{\Delta }x=\gamma (\mathrm{\Delta }{x}^{\prime }+v\mathrm{\Delta }{t}^{\prime }),\mathrm{\Delta }y=\mathrm{\Delta }{y}^{\prime },\mathrm{\Delta }z=\mathrm{\Delta }{z}^{\prime },\mathrm{\Delta }t=\gamma (\mathrm{\Delta }{t}^{\prime }+\beta \mathrm{\Delta }{x}^{\prime }/c),}$$

(C.16)

$$\boxed{\mathrm{\Delta }{x}^{\prime }=\gamma (\mathrm{\Delta }x-v\mathrm{\Delta }t),\mathrm{\Delta }{y}^{\prime }=\mathrm{\Delta }y,\mathrm{\Delta }{z}^{\prime }=\mathrm{\Delta }z,\mathrm{\Delta }{t}^{\prime }=\gamma (\mathrm{\Delta }t-\beta \mathrm{\Delta }x/c).}$$

(C.17)

The differences $\mathrm{\Delta }$ can be finite because the Lorentz transform is linear. This makes the differential Lorentz transform easy to apply to physical problems such as determining the lengths of rulers.

The phenomenon of relativistic time dilation follows from the differential time transform $\mathrm{\Delta }t=\gamma (\mathrm{\Delta }{t}^{\prime }+\beta \mathrm{\Delta }{x}^{\prime }/c)$. If successive ticks of a clock at rest in the primed frame (so $\mathrm{\Delta }{x}^{\prime }=0$) are separated by $\mathrm{\Delta }{t}^{\prime }=1$ in time, they will be separated by $\mathrm{\Delta }t=\gamma \ge 1$ in the unprimed frame. Likewise a clock at rest in the unprimed frame appears to run slow by the same factor $\gamma$ when observed in the primed frame.

Relativistic length contraction can also be derived from Equation C.16. Suppose the ends of a ruler of unit length in the primed frame ($\mathrm{\Delta }{x}^{\prime }=1$) emit two flashes of light at the same time in the unprimed frame ($\mathrm{\Delta }t=0$). The time $\mathrm{\Delta }{t}^{\prime }$ between the flashes in the primed frame can be calculated from $\mathrm{\Delta }t=0=\gamma (\mathrm{\Delta }{t}^{\prime }+v\mathrm{\Delta }{x}^{\prime }/c^2)$ to be $\mathrm{\Delta }{t}^{\prime }=-v\mathrm{\Delta }{x}^{\prime }/c^2$. The ruler length in the unprimed frame is the distance between the flashes. It is shorter by the factor

$$\frac{\mathrm{\Delta }x}{\mathrm{\Delta }{x}^{\prime }}=\frac{\gamma (\mathrm{\Delta }{x}^{\prime }+v\mathrm{\Delta }{t}^{\prime })}{\mathrm{\Delta }{x}^{\prime }}=\gamma (1-{\beta }^2)=1/\gamma .$$

(C.18)

A ruler at rest in the unprimed frame also appears to be shorter by the factor $1/\gamma$ when observed in the primed frame.

Relativistic velocities do not add linearly. Let the velocity of a particle be $\overrightarrow{u}=(u_x,u_y,u_z)$ in the unprimed frame and $\overrightarrow{u^{\prime }}=(u_x^{\prime },u_y^{\prime },u_z^{\prime })$ in the primed frame:

$$u_x\equiv \frac{dx}{dt}=\frac{dx}{d{t}^{\prime }}\frac{d{t}^{\prime }}{dt}.$$

(C.19)

The differential Lorentz transforms $dx=\gamma (d{x}^{\prime }+vd{t}^{\prime })$ and $dt=\gamma (d{t}^{\prime }+\beta d{x}^{\prime }/c)$ yield

	${\displaystyle \frac{dx}{d{t}^{\prime }}}$	$=\gamma \left({\displaystyle \frac{d{x}^{\prime }}{d{t}^{\prime }}}+v\right)=\gamma (u_x^{\prime }+v),$		(C.20)
	${\displaystyle \frac{dt}{d{t}^{\prime }}}$	$=\gamma \left(1+{\displaystyle \frac{\beta }{c}}{\displaystyle \frac{d{x}^{\prime }}{d{t}^{\prime }}}\right)=\gamma \left(1+{\displaystyle \frac{v{u}_x^{\prime }}{c^2}}\right),$		(C.21)

so

$$\boxed{u_x=\frac{u_x^{\prime }+v}{(1+v{u}_x^{\prime }/c^2)}}$$

(C.22)

and, by symmetry,

$$\boxed{u_x^{\prime }=\frac{u_x-v}{(1-v{u}_x/c^2)}.}$$

(C.23)

For the velocity components perpendicular to $v$,

$$u_y\equiv \frac{dy}{dt}=\frac{dy}{d{t}^{\prime }}\frac{d{t}^{\prime }}{dt}=\frac{d{y}^{\prime }}{d{t}^{\prime }}\frac{d{t}^{\prime }}{dt},$$

(C.24)

so

$$\boxed{u_y=\frac{u_y^{\prime }}{\gamma (1+v{u}_x^{\prime }/c^2)}\mathit{\hspace{1em}}\mathrm{and}\mathit{\hspace{1em}}{u}_z=\frac{u_z^{\prime }}{\gamma (1+v{u}_x^{\prime }/c^2)},}$$

(C.25)

and likewise,

$$\boxed{u_y^{\prime }=\frac{u_y}{\gamma (1-v{u}_x/c^2)}\mathit{\hspace{1em}}\mathrm{and}\mathit{\hspace{1em}}{u}_z^{\prime }=\frac{u_z}{\gamma (1-v{u}_x/c^2)}.}$$

(C.26)

The ratio of a moving object’s relativistic mass $m$ to its rest mass $m_0$ follows from a thought experiment in Rindler [91]. Imagine two identical electrons, one at rest in the unprimed frame and the other at rest in the primed frame moving with velocity $v$. Let one electron be slightly displaced from the other along the $y$-axis. At the moment the electrons pass by each other, their Coulomb repulsion will accelerate them in the $\pm y$-directions. Because $dy=d{y}^{\prime }$, both electrons must experience the same $y$ displacement, but time dilation will make the moving electron take a factor $\gamma$ longer to do so. Invoking momentum conservation, both observers conclude that the mass of the electron at rest in the moving frame is a factor $\gamma$ larger:

$$m=\gamma m_0.$$

(C.27)

Likewise, its total energy

$$E=m{c}^2=\gamma m_0{c}^2$$

(C.28)

has been multiplied by $\gamma$. Applying the chain rule for derivatives to the mass–energy transform,

$$P\equiv \frac{dE}{dt}=\frac{dE}{d{t}^{\prime }}\frac{d{t}^{\prime }}{dt}=\frac{dE}{d{E}^{\prime }}\frac{d{E}^{\prime }}{d{t}^{\prime }}\frac{d{t}^{\prime }}{dt}=\gamma P^{\prime }{\gamma }^{-1}=P^{\prime }$$

(C.29)

shows that power is a relativistic invariant.