Next: Practical Applications of a Relational Database of FITS Keywords
Previous: Synthetic Images of the Solar Corona from Octree Representation of 3-D Electron Distributions
Up: Modeling
Table of Contents - Index - PS reprint
Astronomical Data Analysis Software and Systems VI
ASP Conference Series, Vol. 125, 1997
Editors: Gareth Hunt and H. E. Payne
I. C. Busko
Space Telescope Science Institute,
Baltimore, MD 21218, E-mail: busko@stsci.edu
Abstract:
The fitting package in STSDAS (Space Telescope Science Data
Analysis System) relies on two basic techniques (one linear and
one non-linear) for fitting functions to data. In this work, the
statistical properties of both the fitted function coefficients and
their errors are examined, using a Monte Carlo approach. Results
show that both methods may generate biased coefficients
(at the ~few percent level), and over or under-estimate error bars
(at the ~10 percent level), in particular from low signal-to-noise
data.
The two basic techniques used in the STSDAS fitting package are:
(i) linear functions (Legendre and Chebyshev polynomials, cubic
splines) are fitted by minimizing 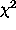 , solving the normal
equations by the Cholesky method. Function coefficient errors are
computed directly from the covariance matrix. This technique is
provided by the IRAF (Image Reduction and Analysis Facility) library
curfit.
(ii) any function, linear or non-linear in its coefficients, can
be fitted by minimizing
, solving the normal
equations by the Cholesky method. Function coefficient errors are
computed directly from the covariance matrix. This technique is
provided by the IRAF (Image Reduction and Analysis Facility) library
curfit.
(ii) any function, linear or non-linear in its coefficients, can
be fitted by minimizing 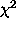 using the downhill simplex
method, also known as amoeba. This method is unable by design
to compute coefficient errors. The package relies on an independent
technique ( bootstrap resampling) to estimate these errors.
using the downhill simplex
method, also known as amoeba. This method is unable by design
to compute coefficient errors. The package relies on an independent
technique ( bootstrap resampling) to estimate these errors.
This work aims at assessing the reliability of coefficient estimates
and error bars generated by both methods.
Artificial data sets were generated from two functions: a 3rd degree
power-series polynomial and a sum of two Planck functions.
Each function was replicated 30 times and in each replication an
independent noise realization was added at a fixed signal-to-noise level.
Noise types included pure Gaussian, pure Poisson and a mixture of Gaussian
plus Poisson. A separate, 30-element data set was created for each
signal-to-noise level studied. Signal-to-noise spanned the range from
~1000 down to ~1 in logarithmic steps.
Each individual data set was fitted by the appropriate fitting task
and results were output to tables. The power series polynomial was fitted
by both linear and non-linear methods.
From the 30 measurements of each function coefficient 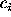 ,
and its estimated error
,
and its estimated error 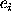 , i = 1, 2 ... 30, three statistics
were computed:
, i = 1, 2 ... 30, three statistics
were computed:
-
The average of coefficient error estimates
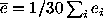
-
The standard deviation of coefficient measurements
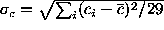
-
The average ``residual'' coefficient (measured minus true)
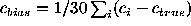
If the coefficient computation is unbiased, 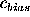 should distribute
itself around zero. If any bias is present, the average of the
should distribute
itself around zero. If any bias is present, the average of the 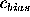 distribution
will depart from zero. On the same grounds, if the coefficient error
estimates are unbiased, that is, if they reflect the population true
standard deviation, the difference
distribution
will depart from zero. On the same grounds, if the coefficient error
estimates are unbiased, that is, if they reflect the population true
standard deviation, the difference 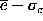 should also distribute itself around zero.
should also distribute itself around zero.
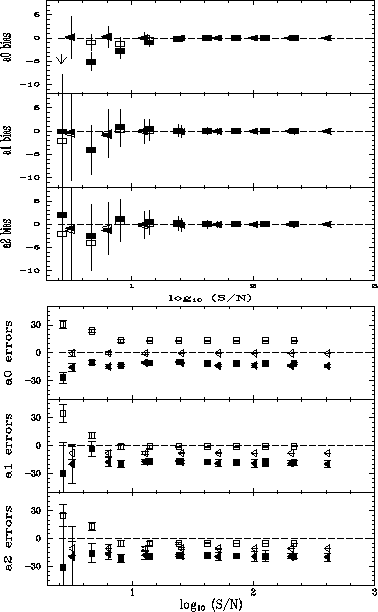
Figure:
Power-series polynomial bias and errors.
Ordinate is ``estimated - true'' coefficient residual
(upper panel) and error bar (lower panel),
in a relative (percent) scale, for the three first lower-order polynomial
coefficients.
Abscissa is signal-to-noise.
Each point depicts the average of 30 measures; error bar depicts the
standard deviation of the same 30 measures.
Solid symbols: non-linear algorithm.
Open symbols: linear algorithm.
Squares: Poisson noise.
Triangles: Gaussian noise.
Points below the zero line mean that the coefficient (or its error)
is systematically underestimated; above the line it is overestimated.
Original Postscript figures(112kB), (64kB).
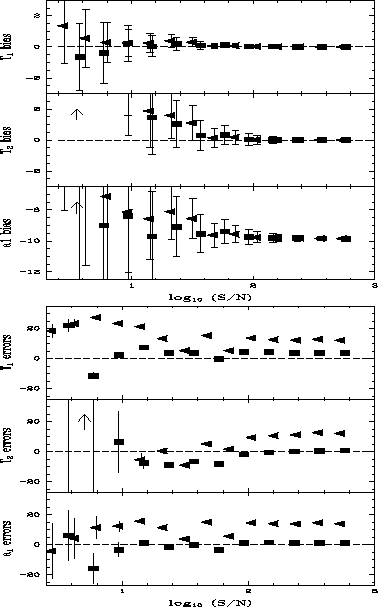
Figure:
Double Planck function bias and errors. The two temperatures and the
largest black-body amplitude are depicted.
See caption for Figure 1.
Original Postscript figures(128kB), (136kB).
Results are summarized in the Figures.
When applied to a power-series polynomial with Gaussian noise, both linear
and non-linear techniques generated unbiased coefficients at the level of
<1% for any tested S/N ratio. Poisson noise introduced underestimation
bias at a level of a few percent for lower (~2-5) S/N data.
The largest bias was seen on polynomial's zero-order term, induced perhaps
by the non-symmetric nature of the Poisson distribution.
A different behavior was seen when fitting the strongly non-linear sum of
two Planck functions. The dominant (in intensity) black-body had its
temperature determined with almost no bias down to S/N ~ 2.
The weaker component, however, showed significant overestimation bias
at low S/N. The dominant black-body's amplitude showed large
(~8-10%) underestimation bias, and the weaker amplitude did not give
significant results. This can be interpreted as the result of both
amplitudes being confused into a single one by the fitting algorithm, thus
resulting in a biased estimate for one of them. The noise model seems to play
no role in these results.
When fitted by the non-linear algorithm, the power-series polynomial
errors showed a systematic underestimation of ~10-20 percent,
seemingly independent of noise type. The linear algorithm, on the other
hand, delivers errors which are off from the ``true'' ones by amounts
that depend on noise type, and might also depend on the coefficient values
themselves.
The double black-body function fit showed errors that lie close to
the true ones in the Gaussian noise case, and with systematic
overestimation of ~20 percent in the Poisson noise case.
As a general rule one might say that bias at a few percent level
should be expected when fitting either non-linear functions, or linear
functions with Poisson noise, in particular with low S/N data.
Also, error bars generated by both linear and non-linear methods are prone
to under or overestimate the ``true'' errors by as much as 10-20 percent,
even with high S/N data. The details, though, seem to be dependent on the
functional form and noise type.
© Copyright 1997 Astronomical Society of the Pacific,
390 Ashton Avenue, San Francisco, California 94112, USA
Next: Practical Applications of a Relational Database of FITS Keywords
Previous: Synthetic Images of the Solar Corona from Octree Representation of 3-D Electron Distributions
Up: Modeling
Table of Contents - Index - PS reprint
payne@stsci.edu
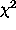 , solving the normal
equations by the Cholesky method. Function coefficient errors are
computed directly from the covariance matrix. This technique is
provided by the IRAF (Image Reduction and Analysis Facility) library
curfit.
(ii) any function, linear or non-linear in its coefficients, can
be fitted by minimizing
, solving the normal
equations by the Cholesky method. Function coefficient errors are
computed directly from the covariance matrix. This technique is
provided by the IRAF (Image Reduction and Analysis Facility) library
curfit.
(ii) any function, linear or non-linear in its coefficients, can
be fitted by minimizing 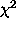 using the downhill simplex
method, also known as amoeba. This method is unable by design
to compute coefficient errors. The package relies on an independent
technique ( bootstrap resampling) to estimate these errors.
using the downhill simplex
method, also known as amoeba. This method is unable by design
to compute coefficient errors. The package relies on an independent
technique ( bootstrap resampling) to estimate these errors.
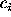 ,
and its estimated error
,
and its estimated error 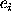 , i = 1, 2 ... 30, three statistics
were computed:
, i = 1, 2 ... 30, three statistics
were computed:
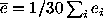
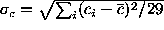
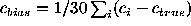
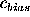 should distribute
itself around zero. If any bias is present, the average of the
should distribute
itself around zero. If any bias is present, the average of the 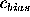 distribution
will depart from zero. On the same grounds, if the coefficient error
estimates are unbiased, that is, if they reflect the population true
standard deviation, the difference
distribution
will depart from zero. On the same grounds, if the coefficient error
estimates are unbiased, that is, if they reflect the population true
standard deviation, the difference 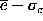 should also distribute itself around zero.
should also distribute itself around zero.

