Next: The Grid Signal Processing System
Previous: A Home-Grown But Widely-Distributed Data Analysis System
Up: Software Systems
Table of Contents - Index - PS reprint
Tim Cornwell
National Radio Astronomy Observatory, PO Box 0, Socorro, NM 87801, E-Mail:
tcornwel@nrao.edu
Mark Wieringa
Australia Telescope National Facility, Locked Bag 194,
Narrabri, NSW 2390, Australia, E-Mail: mwiering@atnf.csiro.au
The processing of data from synthesis arrays has become increasingly sophisticated in recent years, so much so that the final performance of such telescopes is inextricably wedded to the performance of the algorithms used to process the data. Furthermore, some telescopes, such as the proposed Millimeter Array and the Square Kilometer Array, are hard to envisage in operation without the necessary processing algorithms. The drawback to this development is that as the algorithms have increased in sophistication, the difficulty of implementing them in existing packages has increased correspondingly. This difficulty is of course one of the motivations for the AIPS++ Project, in which object-oriented techniques have been adopted with the goal of simplifying development and maintenance of processing algorithms.
AIPS++ is a package for (principally radio) astronomy processing, written in C++ by a collaboration formed between a number of organizations. Those now actively involved are:
AIPS++ is scheduled to undergo a Beta release in early 1997, followed by a limited public release about six months later. More information on AIPS++ may be obtained from the AIPS++ On-Line Documentation page.
The user specifications for AIPS++ were written in late 1991, based upon contributions from a large number of astronomers from the AIPS++ consortium. It is fair to say that the specifications cover all known and some speculative processing algorithms. As well as providing specific functionality in the form of applications, it was also desired that the AIPS++ system provide a means for long-term development of entirely new processing algorithms. The goals for the support of synthesis processing in AIPS++ can be summarized as follows:
Such open-ended flexibility is very demanding of the design of the system, and requires that the abstraction of synthesis telescopes be as general as possible. Thus, ambition drives the level of abstraction higher and higher. However, too high a level of abstraction is difficult to work with and so some compromise must be found. Early attempts to find the correct level of abstraction were not entirely successful. One of the authors advocated an approach based upon the linear mathematics common to all imaging telescopes. A better approach, and one that the Project eventually adopted, is to base the abstraction on the physics of synthesis arrays. In this paper, we present the details of the physical model for synthesis arrays that was adopted. We describe how this was translated into an object-oriented design, and how that design was implemented in AIPS++. We also show some examples of synthesis data processed using this framework. First, we must briefly review synthesis calibration and imaging.
Interferometric arrays measure the Fourier transform of the Sky Brightness:
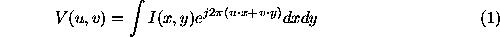
In practice, this transform is sampled only at a limited number of discrete points, and it is typically corrupted by antenna-based calibration errors:
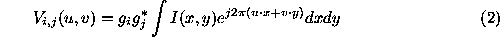
Calibration and imaging in radio interferometry corresponds to solving for the calibration parameters g and the sky brightness I. There are many special cases where these equations must be modified:
The simple two-dimensional Fourier transform has been generalized in many different ways. Ultimately, it can be derived from the law for the propagation of mutual coherence in optics and the van Cittert-Zernike equation. Hamaker, Bregman, & Sault (1996) came across one very useful generalization by considering the polarization properties of synthesis arrays.
The required changes to the above equations must take into account the following:
The Hamaker-Bregman-Sault Measurement Equation does take these into account. It is expressed in direct products of 2×2 matrices (Jones Matrices) representing the antenna-based calibration effects, and 4 vectors representing the measured coherence and sky brightness:
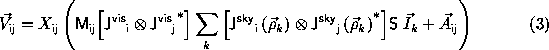
where:
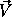
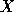
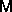
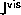
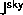
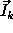
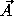
Not surprisingly, this equation does specialize to the usual Fourier
transform equation between sky brightness, and furthermore, by the
correct choice of the components, such as the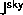 
, one can
derive other imaging modes, such as mosaicking.
For this equation to be useful in handling general problems of calibration and imaging, we need to be able to do the following things:
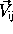if given all terms on right
hand side,
Before proceeding further, it is a good idea to split this one equation into separate Sky and Vis Equations:
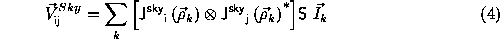
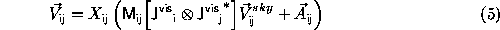
We now also have to make some choice about the class of algorithms that we wish to support. For the moment, we have chosen to limit the main support to those algorithms that can be related to least-squares methods. Perhaps surprisingly, this accommodates many different calibration and imaging algorithms.
For simplicity, consider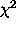 
for one time interval:
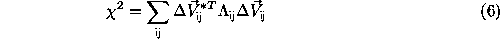
A large class of algorithms, including Maximum Entropy, optimize some
combination of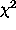 
and another term. For these, one requires the
derivatives of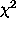 
with respect to the unknown pixels:
Another whole class of algorithms, represented by CLEAN, require a residual image of some sort. A little thought convinces one that a generalized residual image can be defined as:
The utility of this generalized residual image is that it may be used in many iterative-update type algorithms in which a trial estimate image is updated from the residual image.
Note that the corresponding PSF may well not be shift-invariant, and so either some approximation must be used or the algorithm must accommodate a shift-variant PSF.
Many calibration algorithms require derivatives of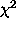 
with
respect to the various gain matrices. As an example, consider the case
where only one term is required:
where the matrix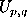 
is unity for element 
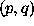and zero
otherwise.
These gradients may be used in a least squares solution for the calibration parameters.
In an object-oriented system, one would want to provide services to evaluate these gradients (and the original equations) for quite general forms of the components of the equations. The interface of the components need only be specified as far as it concerns the calculation of these quantities. Otherwise, the behavior of the components is unspecified, and may be varied to suit different contexts.
A consumer of these services has to be responsible for the
model or trial estimates but not for evaluating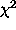 
and
associated gradients.
The support for the Hamaker-Bregman-Sault Measurement Equation is provided by a number of C++ classes:
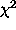, and the gradients of 
,
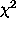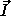to the SkyEquation
class,
,
,
,
,
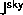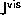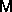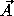and
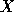to a 4 vector.
The MeasurementComponents SkyModel , SkyJones , VisJones , MIfr , ACoh , and
XCorr can solve for themselves given a specific SkyEquation or VisEquation and VisSet .
Programmers write special versions of these MeasurementComponents
for particular circumstances. As a concrete example, consider the
calibration of a phase screen across a compact array such as the
proposed Millimeter Array. In conventional self-calibration procedures,
one would solve for the phases of all 40 antennas. A more sensible and
robust approach is to solve only for a limited number of parameters
describing a phase screen across the array. This could be simply a
tilted screen or perhaps a few curvature terms, but the main point is
that since the number of degrees of freedom would be limited, the
robustness and sensitivity would both improve. In the AIPS++ approach,
the programmer merely has to develop a MeasurementComponent that uses
the VisEquation services to get gradients of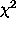 
for the relevant Jones
matrices, and converts this gradient information into update information
for parameters of the phase screen. The interface to the VisEquation is thus fixed,
but the internal behavior of the component is unspecified.
A similar approach works for the SkyModel . Here all the gradients are calculated in terms of a discrete pixellated images, but any given SkyModel may use these gradients as desired, perhaps to drive the solution for the parameters of Gaussian components.
Simulation is straightforwardly accommodated by providing MeasurementComponents that generate, rather than solve for, instrumental effects.
The design of the applications level code has been through a number of revisions. We initially used a monolithic, command-line program with lots of switches to control behavior-the prime advantage of this approach is simplicity: one could exercise all of the code this way. For the end-user, it has one prime drawback: the behavior of the application is controlled by a number of switches and it is hard to understand and document. Despite these shortcomings, it is still the best way to write a test program.
With this in mind, we changed the design to be based upon objects that could be directly invoked from the AIPS++ CLI, Glish, using the AIPS++ Distributed Object mechanism. By decomposing the code from the monolithic applications, we derived objects with different responsibilities, all coded in terms of the underlying C++ classes. The five user-level objects were:
calibrater:=imager.calibrater(); calibrater.initialize(calibrater, '3C273XC1.MS'); calibrater.set(calibrater, 'P', 30.0); calibrater.correct(calibrater); calibrater.write(calibrater);
In the final revision of the application code, we watched what people did and then built standard sequences of object invocations into CLI functions. This is the imager package in AIPS++. A typical example of the use of the imager would be as follows:
include "imager.g" # Include definition of imager and di
di.initialize("3C273XC1") # Initialize inputs
di.getfits() # Get data from the FITS file
di.show() # Show the inputs
di.cell:=0.7 # Cellsize
di.makeimage() # Make an empty template image
di.P.t:=60.0 # Time scale for parallactic angle
di.G.t:=300.0 # Time scale for antenna gain changes
di.D.t:=3600.0 # Time scale for polarization leakage changes
di.initcal() # Set up calibration objects
di.beam:=[2.5, 2.5, 0] # Beam size
di.clean.niter:=10000 # Number of clean iterations
di.deconv() # Perform clean deconvolution
di.dis() # Display the image
for (selfcal in 1:5) # Perform 5 loops of....
{
di.scal() # Perform one selfcal iteration
di.plotres() # Plot residual visibility
di.dis() # Display the image
}
The object di is the default instance of the class imager.
Our next planned step is to build a GUI interface that
invokes these functions and integrates display and plotting.
We performed a detailed analysis of the Hamaker-Bregman-Sault formalism
before starting the design, and read a lot. But in the end, we did not adopt any
formal methodology or diagramming tools. We did lots of prototype
coding, all in C++, although next time, we would probably do at least the
early stages in Glish. We split responsibilities for development in
different areas, and reconciled code divergences, by hand, every few
days. The overall breakup into classes was settled fairly early on and
changed relatively little. The assignment of responsibilities to
classes changed a lot as we looked for and found a natural split of the
evaluation of gradients of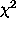 
. This probably represented most of
the experimentation that was performed. Symmetry in the design between
the Jones matrices and the SkyModel was the most powerful organizing
principle that we came upon. Enforcing uniformity of interface across
objects was also important. Finally, we came to the split between SkyEquation
and VisEquation quite late on. While the split was obvious, the reasons for
making the design split became more pressing as we got deeper into the
details and began to think in more detail about, e.g., Single Dish
processing.
Clearly this is not a simple waterfall design process, in which specification leads to analysis, design, implementation, testing, and deployment. Instead it is probably better described in terms of the spiral model whereby one revisits each of the above stages a number of different times, each time having progressed from the last time. The design is still evolving, somewhat, as we try to optimize performance, especially on spectral line datasets. We think that such a spiral design process is mandated by the complexity of the problem that we were trying to solve.
We wrote special classes for matrices with few elements and special symmetries (SquareMatrix) and vectors with few elements (RigidVector). It was necessary to drop into FORTRAN for some inner loops, e.g., FFTs, gridding, and CLEAN loops.
Our conclusions on developing within AIPS++ are as follows. AIPS++ is (currently) very complex but is well-featured. It seems that C++ is a net win but the buy-in is large (6-12 months for competence to do the type of design work presented here). There are many new concepts that one must learn (e.g., iterators) that simply cannot be avoided. Compilers are an obstacle: Gnu is the standard compiler and is the best of the lot. Finally, we found the loose collection of AIPS++ tools united by Glish to be wonderful for development.
We thank Brian Glendenning and Ger van Diepen for advice and help in working inside AIPS++, and Jan Noordam and Johan Hamaker for discussions.
Hamaker, J. P., Bregman, J. D., & Sault, R. J. 1996, A&AS, 117, 137
Next: The Grid Signal Processing System
Previous: A Home-Grown But Widely-Distributed Data Analysis System
Up: Software Systems
Table of Contents - Index - PS reprint