
Figure: Faint background variations revealed after smoothing. Four images are shown for each filter. The two bright objects are stars. Original PostScript figure (1.1MB).
Next: In-Orbit Calibration of the Distortion of the SOHO/LASCO-C2 Coronagraph
Previous: ZGSC (Compressed GSC) and XSKYMAP
Up: Instrument-Specific Software
Table of Contents - Index - PS reprint
Peter Linde and Ralph Snel
Lund Observatory, Box 43, S-221 00 Lund, Sweden,
E-mail: peter@astro.lu.se
A Nordic group (Ardeberg et al. 1997) is using the Hubble Space Telescope in a study of stellar populations in the Bar of the Large Magellanic Cloud (LMC). A total of 35 hours of exposure have been obtained using the WFPC2 camera with Strömgren uvby filters. Through accurate photometry, we determine ages, metallicities, and the luminosity function.
Accurate photometry is essential, and we are investigating various effects affecting the measurements. New algorithms have been developed. Here we present some initial results.
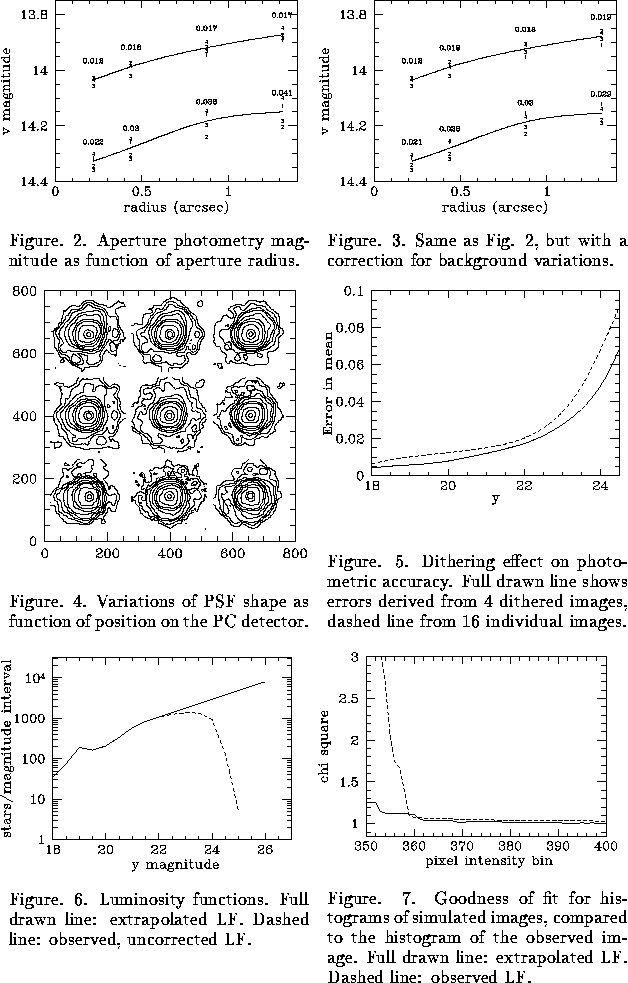
We have noted weak background variations in some of our exposures, typically the shorter ones. Figure 1 shows a set of calibration exposures (with two stars) using the Strömgren uvby filters. In order to see the variations through the noise, the images have been smoothed. The two calibration stars are seen as squares. Typical amplitudes of the background variations are 0.5 ADUs. Aperture photometry results for the v filter, as a function of aperture radius, are shown in Figure 2. The individual frame numbers are given as data points, as well as a standard deviation for each set of points. The spread is larger than expected from photon statistics. A simple attempt to correct for the background variations was made, using an average over all image columns and then reexpanding into a background image. In Figure 3, the corresponding results are given. Only a marginal improvement can be noted.

Figure: Faint background variations revealed after smoothing. Four images
are shown for each filter. The two bright objects are stars.
Original PostScript figure (1.1MB).
Sixteen images were obtained of our target LMC field using the F547M (y) filter. For each set of four exposures, consecutive exposures have a quarter pixel offset with respect to the axes of the detector pixel grid. After reconstruction, this effectively improves the sampling of the image.
We have analysed these data using point spread function (PSF) fitting techniques (Daophot/Allstar, Stetson 1987), both as a set of 16 individual exposures and as four sets of dithered images. Figure 5 shows the mean error as a function of magnitude; the dotted line shows non-dithered results and the solid line shows dithered results. A significant improvement in accuracy is noted. The improvement will be more pronounced in our crowded Wide Field Camera (WFC) images, and may be increased further through use of a more sophisticated method of combining the individual dithered images.
Our analysis allows us to check for point spread function shape variations in the HST Planetary Camera (PC) field. Algorithms were developed to extract PSFs from dithered and oversampled images. Each PSF was defined from approximately 20 stars. Figure 4 shows a sequence of panels with PSFs derived from different parts of the field. In the figure, the grid represents pixel position on the PC detector, with each PSF enlarged a factor of 20. From Figure 4, a noticeable shape change with position is verified. For comparison, see Biretta et al. (1996). We are now analysing the effect on our photometry, and are developing algorithms to properly include this in the data analysis.
In crowded field images, we are deriving information about the faint end of the luminosity function (LF) from the texture of the image background. This algorithm aims at studying objects fainter than can be reached using conventional completeness estimation techniques. Intensity deviations due to many undetectable faint stars are always positive, which will affect the statistical properties of the pixel intensity distribution. From this, the number and the intensity distribution of faint stars can be estimated. Characteristics such as the shape of the PSF, detector noise properties, etc., influence the texture of the background and have to be modeled carefully.
We compare a simulated image to an observed one. If the images are
statistically similar enough, it is assumed that the LFs are similar.
As a measure of similarity, the 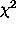 measure between the two
histograms of the simulated and observed images is used. A lower value
of
measure between the two
histograms of the simulated and observed images is used. A lower value
of 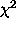 indicates a better fit to the histogram. By iteratively
adjusting and extrapolating the observed LF, simulated images with
increased statistical similarity are created.
indicates a better fit to the histogram. By iteratively
adjusting and extrapolating the observed LF, simulated images with
increased statistical similarity are created.
Figure 6 shows an example of an observed LF derived from a single WFC image, together with a preliminary model LF. The simple model used has two free parameters: the steepness of the LF and the level of the background. Figure 7 shows the statistical differences between histograms derived from the real image, with a background level of 355 ADU, and two simulated images. One was created using the LF derived from standard measurements of the detectable stars. The other was created using the model LF. The decreased chi-square values for the histogram of the latter shows that the model LF is closer than the observed to the true LF.
Ardeberg, A., Gustafsson, B., Linde, P., & Nissen, P.-E. 1997, A&A, in prep.
Biretta, J. A., et al. 1996, WFPC2 Instrument Handbook, vers. 4.0 (Baltimore: STScI)
Stetson, P. B. 1987, PASP, 99, 191
Next: In-Orbit Calibration of the Distortion of the SOHO/LASCO-C2 Coronagraph
Previous: ZGSC (Compressed GSC) and XSKYMAP
Up: Instrument-Specific Software
Table of Contents - Index - PS reprint