Manipulating Vectors and Arrays

 

    The following functions are available for manipulating (primarily numeric) vectors and arrays (see § 3.7.1, page  for information on creating arrays):

length(...)
    returns a vector in which each of the of elements is the length the vector argument, or the number of fields in the argument, if the argument is a record. So,

    length(1:3,5:10,1:10)

returns [3, 6, 10]. length may be abbreviated to len.  

sum(...)
    returns the sum of all of all of its arguments. The arguments must be numeric vectors. For example,

    sum(4:6, 1, 2)

returns 18. The value returned is a double scalar.

An error is generated and F returned if x is not numeric.

prod(...)
    returns the product of all of its arguments. The arguments must be numeric vectors. For example,

    prod(1:3, 1, 2)

returns 12. The value returned is a double scalar.

An error is generated and F returned an argument is not numeric.

   

min(...)
  and max(...)   return the minimum and maximum element of the of all of the numeric vector arguments. For example,

    min(3:5, 1:-3, 6:9)

returns -3. The value returned is a double scalar.

These functions are special cases of the more general function range(...),     which returns a two-element double vector giving the minimum and maximum elements of all of the numeric vector arguments:

    range(1:10)

yields [1, 10], but

    range(1:10,5:90,1:-3)

returns [-3,90].

An error is generated and F returned if x is not numeric.

 

sort(x)
  returns x sorted into ascending order. x must be either numeric or string.

 

sort_pair(x,y)
  rearranges the elements of y to reflect the order of the elements of x (x and y must have the same length). For example,

    sort_pair([3,1,2], "a b c")

yields "b c a", since "b" was paired with the smallest element of [3,1,2], "c" with the second smallest, and "a" with the largest.

 

order(x)
  returns the indices of the sorted elements of x. So, for example,

    x[order(x)] == sort(x).

   

imag(x)
  and real(x)   return the real or imaginary portion of the numeric vector argument, x. For example,

    real(4-9i)

returns 4.

complex(x,y)
    is the inverse of real(x) and imag(x). Given two vectors, this function creates a vector of complex numbers. If the two vectors have the same length the complex numbers are created element by element, taking the real portion from x and the imaginary portion from y. If x or y is a scalar, it is paired with each of the elements of the other. So,

    complex(3:5,-1)

yields [3-1i, 4-1i, 5-1i]. If x is already a complex number, it is simply returned. If either x or y is a double the result is a dcomplex otherwise the result is a complex.

conj(x)
    takes the complex conjugate of x where x is a vector of complex numbers.

arg(x)
    returns the argument of a complex number, i.e. atan( imag(x) / real(x) ).

 

sqrt(x)
, exp(x), log(x), ln(x), sin(x), cos(x), tan(x), asin(x), acos(x), and atan(x)                                         return the square root, exponentiation (i.e., 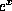), logarithm (base 10), natural logarithm (base e), sine, cosine, tangent, arcsine, arccosine, and arctangent of the numeric vector (array) x, operating on each element in turn. The computation is done on the value of x as coerced to double, and the returned value is a vector (array) of type double. For example,

    sqrt(1:5)

yields [1, 1.41421, 1.73205, 2, 2.23607].

An error is generated and F returned if x is not numeric.

abs(x)
    returns the absolute value of the numeric vector x. The result has the same type as x.

The absolute value of a boolean value is simply that same boolean value.

The absolute value of a complex or dcomplex value, x, is sqrt( real(x)^2 + imag(x)^2 ).

An error is generated and if x is not numeric and an undefined value is returned.

all(x)
    returns T if every element of x is either T (if x's type is boolean) or non-zero (otherwise). It returns F if any element of x is either F or zero. For example,

    all(y > 3)

returns T if-and-only-if every element of y is greater than 3.

An error is generated and if x is not numeric and an undefined value is returned.

any(x)
    is analogous to all(x); it returns T if any element of x is either T or non-zero, and F if every element is F or zero. For example,

    any(y > 3)

returns F if-and-only-if every element of y is less than or equal to 3.

 

seq(x)
    returns an integer vector of all of the numbers between 1 and x if x is a scalar:

    seq(5)

yields [1, 2, 3, 4, 5], as does:

    seq(5.4)

If x is less than 1 or not numeric, an error is generated and F returned.

If x is not a scalar then its length is used instead:

    seq([3, -5, 2])

yields [1, 2, 3]. This version of seq() is often useful for generating vector indices. See examples in § 3.6.2, page , and § 5.5.2, page . In this case x can also be of type string.

seq(x,y)
    starts at x and proceeds counting by 1 until reaching y, returning the result as either an integer vector if x was an integral value (e.g., 3 or 5.0) or else as a double vector. If y is less than x then the function counts downwards.

For example,  

    seq(3,5)

yields [3, 4, 5], while

    seq(5.2, 1)

yields [5.2, 4.2, 3.2, 2.2, 1.2].

If x or y contains more than one element then the first element is used.

If x or y is not numeric then the results are undefined.

seq(x,y,z)
    is similar to the preceding seq(x,y) function except instead of counting by 1, it counts by z. If x is less than y then z must be positive, and if x is greater than y then z must be negative. If z fails this requirement, or if z is 0, then an error is generated and F returned.

For example,

    seq(1,2,.2)

yields [1, 1.2, 1.4, 1.6, 1.8, 2].

  A call to seq() resulting in more than a million elements results in an error message and a return value of F.

See § 3.6.1, page , for other examples of seq().

ind(x)
    returns a vector of indices corresponding to x, which must be either a vector or a record. Thus,

    ind(x)

is equivalent to:

    1:len(x)

rep(value, count)
    takes two parameters the vector value and count. If count is a scalar rep() returns a vector consisting of count copies of value. For example,

    rep(6:5,3)

yields [6, 5, 6, 5, 6, 5]. If, however, count is a vector whose length equals value's length, then it replicates each of the elements of value the number of times specified in the respective element of count. So,

    rep(6:5,2:3)

yields [6, 6, 5, 5, 5], that is it repeats 6 two times, and it repeats 5 three times.

If called with erroneous arguments, rep() reports an error and returns F instead.

array(init, ... )
    this function is used to create n dimensional arrays. The first agument, init, is used to initialize the array. The following arguments specify the length of each of the dimensions of the array. If the length of init is less than the total number of elements of the array, init will be repeated to fill the array, and if its length is greater, only enough of the initial elements of init to fill the array will be used. For example:

    array(0,3,3)

will create a three by three matrix will all of its elements initialized to 0.

cbind(a, b, ... )
    takes any number of parameters which can be either vectors or two dimensional arrays, and it augments a with the subsequent arguments by adding columns to a. If two dimensional arrays are involved, they must have the same number of rows; otherwise, an error message will be generated, and the operation will fail. Here is an example of binding matricies and vectors:

    cbind(array([1,2],2,2),array([3,4],2,2),10:20)

It yields the output:

    [[1:2,]
        1 1 3 3 10
        2 2 4 4 11]

Note that the extra elements of vectors are ignored. cbind can be used with vectors alone:

    cbind(1:6, 100:20, 3:5, 8:0)

yeilds:

    [[1:3,]
        1 100 3 8
        2 99  4 7
        3 98  5 6]

rbind(a, b, ... )
    takes any number of parameters which can be either vectors or two dimensional arrays, and it augments a with the subsequent arguments by adding rows to a. If two dimensional arrays are involved, they must have the same number of columns; otherwise, an error message will be generated, and the operation will fail. This very similar to cbind. Here is an example:

    rbind(array([1,2],2,2),20:10)

This example generates the following output:

    [[1:3,]
        1  1
        2  2
        20 19]