


Next: 3.8 Fitting and optimization
Up: 3 The model
Previous: 3.6 Field ordering
3.7 Model integration
The principal steps in calculating the brightness distributions are as
follows:
- Construct grids to match the observations at each of the two
resolutions.
- At each grid point, determine whether the line of sight passes
through the jet. If so, calculate the integration limits corresponding to
the outer surface of the jet and, if relevant, the spine/shear-layer
interface. Separate ranges of integration are required to avoid
discontinuities in the integrand.
- Integrate to get the Stokes parameters I, Q
and
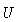 using Romberg
integration. The steps needed to determine the integrand
are outlined below.
using Romberg
integration. The steps needed to determine the integrand
are outlined below.
- Add in the core as a point source.
- Convolve with a Gaussian beam to match the resolution of the
observations.
- Evaluate
 over defined areas, using an estimate of the
``noise level'' derived as described later.
over defined areas, using an estimate of the
``noise level'' derived as described later.
In order to determine the I, Q and U emissivities at a point on the line
we follow an approach described in detail in
Laing 2002 and based on that
of Matthews & Scheuer (1990).
We neglect synchrotron losses, on the grounds that the
observed spectrum is a power law with 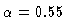 between 1.4 and
8.4 GHz (and extends to much higher frequencies;
Hardcastle et al. 2002).
The emissivity function
between 1.4 and
8.4 GHz (and extends to much higher frequencies;
Hardcastle et al. 2002).
The emissivity function
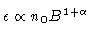 , where B is
the total field and n0 is the normalizing constant in the electron
energy distribution as defined in Section 3.1. The observed
emissivity can be calculated in the formalism developed by
Laing (2002) by
considering an element of fluid which was initially a cube containing
isotropic field, but which has been deformed into a cuboid by stretching
along the three coordinate directions by amounts proportional to the field
component ratios in such a way that the value of
, where B is
the total field and n0 is the normalizing constant in the electron
energy distribution as defined in Section 3.1. The observed
emissivity can be calculated in the formalism developed by
Laing (2002) by
considering an element of fluid which was initially a cube containing
isotropic field, but which has been deformed into a cuboid by stretching
along the three coordinate directions by amounts proportional to the field
component ratios in such a way that the value of 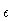 is
preserved. We calculate the synchrotron emission along the line of sight
in the fluid rest frame, thus taking account of aberration.
is
preserved. We calculate the synchrotron emission along the line of sight
in the fluid rest frame, thus taking account of aberration.
The main steps in the calculation are:
- Determine coordinates in a frame fixed in the jet, in particular the
radial coordinate
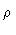 and the streamline index
and the streamline index 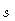 , numerically if
necessary.
, numerically if
necessary.
- Evaluate the velocity at that point, together with the components of
unit vectors along the streamline coordinate directions (and hence the
angle between the flow direction and the line of sight
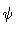 ). Derive
the Doppler factor
). Derive
the Doppler factor
![$D = [\Gamma (1 - \beta\cos \psi)]^{-1}$](img151.gif) and hence the
rotation due to aberration (
and hence the
rotation due to aberration (
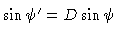 , where
, where
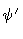 is measured in the rest frame of the jet material). Rotate
the unit vectors by
is measured in the rest frame of the jet material). Rotate
the unit vectors by
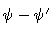 and compute their direction
cosines in observed coordinates.
and compute their direction
cosines in observed coordinates.
- Evaluate the emissivity function
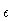 and the rms components
of the magnetic field along the streamline coordinate directions
(normalized by the total field). Scale the direction cosines derived in
the previous step by the corresponding field components, which are
and the rms components
of the magnetic field along the streamline coordinate directions
(normalized by the total field). Scale the direction cosines derived in
the previous step by the corresponding field components, which are
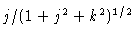 (radial),
(radial),
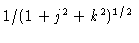 (toroidal) and
(toroidal) and
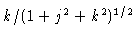 (longitudinal) in the notation of the previous
section.
(longitudinal) in the notation of the previous
section.
- Evaluate the position angle of polarization, and the rms field
components along the major and minor axes of the probability density
function of the field projected on the plane of the sky (Laing 2002).
Multiply by
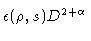 , to scale the emissivity and
account for Doppler beaming.
, to scale the emissivity and
account for Doppler beaming.
- Derive the total and polarized emissivities using the expressions
given by Laing 2002 and convert
to observed Stokes Q and
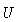 .
.
