3.9 Uniqueness

As with any model-fitting procedure, questions of uniqueness must be considered. Our approach is an advance on previous attempts at jet velocity estimation in several respects:

1. We seek to fit a large quantity of well-resolved two-dimensional data, rather than one-dimensional profiles.
2. We have detected both jets at all distances from the nucleus, and do not have to cope with upper limits.
3. We fit linear polarization (Stokes Q and U) and total intensity (Stokes 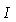$I$) simultaneously with a small number of free model parameters. Although this introduces further degrees of freedom in order to describe the field anisotropy, we find that the form of the jet velocity field is as severely constrained by the observed polarization data as by the jet sidedness - the more traditional quantity used to infer jet velocities.

Model images that even qualitatively resemble the observations are hard to find. Although the downhill simplex algorithm is not guaranteed to converge on a global minimum in $\chi ^2$, we experimented with a wide range of initial conditions and found no other significant minima. We are therefore confident that the parameters given in the next section describe a unique solution.

2002-06-13