Darrel Emerson,
Mathcad Worksheet
5 Feb 1998.
Background: the worst case of ellipticity is introduced by propagation at right angles to the magnetic field, with the E-field vector of the incident plane polarized wave at 45 degrees to the magnetic field. This wave can be considered as the superposition of two linearly polarized waves, one with the E-field vector parallel to the magnetic field and the other with the E-field at right angles to the magnetic field. These waves are essentialy the ordinary, and the extraordinary components for propagation transverse to the magnetic field.
For the ordinary wave, the E-field accelerates electrons parallel to the magnetic field, which means that the magnetic field has no influence - a magnetic field only imposes a force on charged particles moving perpendicular to the field.
For the extraordinary wave, the E-field of the incident radiation accelerates the free electrons normal to the magnetic field, which then exerts a force on the electrons and so modifies the electronic motion. This causes the refractive index of the extraordinary wave to be different from that of the ordinary wave.
The different refractive indices of the two component waves, meaning different velocities, causes a progressive phase shift between the two components. If this phase shift becomes 90 degrees, then the initial 100% linearly polarized wave has been turned into a 100% circularly polarized wave. For smaller differential phase shifts, the wave becomes ellipticaly polarized.
The ionosphere can conveniently be characterised by the gyro frequency and the plasma frequency.
Gyro or cyclotron frequency:
fg = ![]()
Plasma frequency: fp =
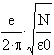
where e and m are the charge and mass of the electron,
B is the earth's magnetic field
N is the number of charged particles per cubic meter
![]() is
the permittivity of a vacuum.
is
the permittivity of a vacuum.
with the earth's field at about 0.5 Gauss, fg is approximately 1.4 MHz
fp approximates to ![]()
A typical value of N is
![]()
![]() which makes fp typically about 9 MHz.
which makes fp typically about 9 MHz.
![]()
We will consider a linearly polarised wave, propagating transverse to the earth's magnetic field, and with the E-field at 45 degrees to the magnetic field direction. This can be considered as the sum of two linearly polarised waves, in phase, one with the E-field parallel to the magnetic field and the other perpendicular to the magnetic field. These two components (the ordinary ray and the extraordinary ray) have different refractive indices, Ro and Re given by:
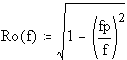
where ![]() is the signal frequency in Hz.
is the signal frequency in Hz.
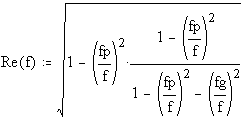
The difference in phase after two waves have propagated a free-space distance D through different refractive indices Ro and Rf is:
![]()
or where c is the velocity
of light ![]() m/s
m/s
![]()
Inverting this, to find the distance d required to give a certain differential phase difference:
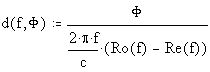
with d in meters.
or
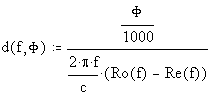
with d in km
To give 100% circular polarization, the phase shift must be 90 degrees, or
![]() radians.
radians.
This assumes the E-field of the components parallel to, and perpendicular to, the magnetic field lines are equal - in other words, the wave is linearly polarized at 45 degrees to the field.
| AR | Phase diff. | 50 MHz | 144 MHz | 432 MHz |
|---|---|---|---|---|
| Circular polarization: | ||||
| 0 dB |
|
|
|
|
| Elliptical polarisation: | ||||
| 6 dB |
|
|
|
|
| 10 dB |
|
|
|
|
| 20 dB |
|
|
|
|