Darrel Emerson
(Extracts From Mathcad worksheet)
Feb 1998
Last modified May 31 1998
(Apologies for the poor format conversion from Mathcad .mcd into .html format)
Plasma angular frequency: choose typical value of 10 MHz:
Gyro angular frequency (cyclotron frequency): choose typical 1.4 MHz.
Define parameters X, Y and Z, to be used in calculations below:
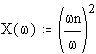
![]()
Define YL and YT, the longitudinal and transverse components.
theta = 0 for purely longitudinal propagation (i.e. along the magnetic field lines),
theta = pi/2 for purely transverse propagation, perpendicular to the magnetic field lines
In this case, we only consider longitudinal propagation, so:
![]()
![]()
Now introduce the effective collision frequency. Collisions are responsible for attenuation in the ionosphere. The effective collision frequency can range from 103 to 108, with lower values giving highest differential absorption between LHCP and RHCP components. If the effective collision frequency is much less than the signal frequency (which is certainly true for VHF frequencies), the precise value is of very little consequence in determining the differential absorption ratio.
n
is the effective collision frequency. Set to 104![]()
![]()
If fsig is the signal frequency, then the angular signal frequency is:
![]()
From Hunsucker, Radio Techniques for Proving the Terrestrial Ionosphere, R.D. Hunsucker, Springer Verlag (1991), p.47 (Equation 2.26), the magnetoionic dispersion equation is given by:
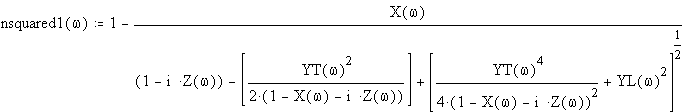
and
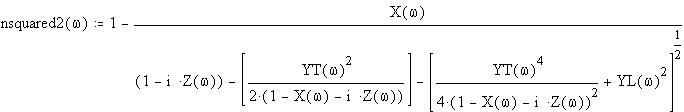
In terms of the complex refractive indices, the two absorption coefficients are given by (e.g. Lang, Astrophysical Formulae, p.56):
![]()
![]()
where c is the velocity of light (m/s)
The ratio of absorption coefficients of the ordinary and extraordinary rays is given by:
![]()
which, since 1 neper is by definition a constant number (8.686) of dB, means that the ratio of attenuation in dB is the same value. i.e.:
dBnepers is the ratio of dB to napers, for a given attenuation.![]() i.e.:
i.e.:
![]()
![]()
Check: from Chatterjee (Propagation of Radio Waves, B.Chatterjee, Asia Publishing House (New York) 1963) p.49, the ratio of absorption coefficients is given by:
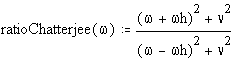
It can be shown that this expression from Chatterjee is identical to that derived here (rationeper) directly from the magnetoionic dispersion relationships.
In other words,
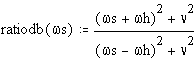
The actual loss in dB, given the absorption coefficient and the distance L, is given for the ordinary and extraordinary rays by:
![]()
![]()
Given the attenuation of the ordinary ray in dB or in nepers, the attenuation of the extraordinary ray in the same units will be rationeper = radiodB larger
The ratio of electric field in the ordinary and extraordinary rays, Eratio, for a given attenuation A of the ordinary ray and Ae of the extraordinary ray, will be given by:
![]()
![]()
A circularly polarised wave with rotating E-field E can be split into equal Ex and Ey terms. E1x and E1y are the vertical and horizontal terms of the RHCP component, while E2x and E2y are the vertical and horizontal terms of the LHCP component.
Assuming unity amplitude of the RHCP E-field, then:
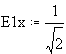
![]()
![]()
![]()
Note the negative sign in E2y, for LHC vs RHC
Calculating the Axial Ratio of an elliptically polarized wave:
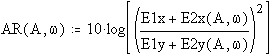
where AR is in dB, and the major and minor axes of the ellipse coincide with the X and Y (vertical and horizontal) axes.
Calculations
The effective collision frequency is set to to 104. This is a relatively low value, which will tend make the apparent differential absorption greater - i.e. an upper limit.
![]()
| Frequency, Hz | Ordinary ray attenuation, dB | Extraordinary ray attenuation, dB | Axial Ratio, dB |
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|