The Collisionless Boltzmann Equation

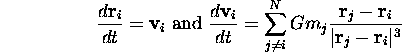
We define a galaxy as a self gravitating system of stars and particles of dark matter (Barnes, 1996). The Newtonian equations of motion for such a system may be written as:

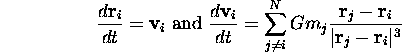
where we are considering N point masses; refers to the position of the ith mass, refers to the velocity of the ith mass and m is the mass of the ith particle. G is the gravitational constant. However, it is far more convenient to adopt a continuous treatment of the system; when one considers typical values of for a globular cluster or for an average sized galaxy, it should be clear that Newton's equations are far too general!

By adopting this continuous description, we need not specify masses, positions and velocities for all N particles; instead, we define a mass distribution and work in a 6N dimensional phase space. The mass at a point at a time t can now be defined in terms of the distribution function or phase space denisty as:

Furthermore, we can distinguish between stars and dark matter by writing the distribution function as:

where is the stellar distribution function and is the dark matter distribution function.

It should be clear that everyone in phase space. In order to find the dynamical equation for the distribution function, we assume that the flow of matter through the 6N dimensional phase space is governed by the smooth 6-dimensional vector field:

where is the gravitational potential.

By the conservation of mass:

Furthemore:

This is the Collisionless Boltzmann Equation(also called the Vlasov Equation) and is a special case of Liouville's Theorem. Essentially, the CBE states that the flow of stellar phase points through phase space is incompressible, or the phase space density around the phase point of any star remains constant.

The CBE is used in conjunction with Poisson's Equation for the gravitational field:

where is any mass not described by the distribtion function f.