Galactic mergers are some of the most dynamic events in the universe. Tidal (just gravitational) forces strip stars and gas out of a galaxy into elegant tidal features while other material is compressed causing copious star formatio n. The fact that all these effects are the result of simple gravity is astonishing.
For many years, scientists did not believe that the features seen
in peculiar galaxies could possibly be the result of Newton's simple
gravitational law, Fg = G M m / r^2. (Newton, 1726, Royal Academic
Society) There were various theories that related these features to the
jets seen in distant radio objects. Looking at Figure 1 (left),
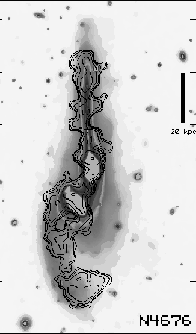
a picture of NGC 4676, or "The Mice", one can understand where they
would get such an impression. The northern tail extends straight out
from the top, why shouldn't that be a jet?
Astrophysicists were led back to simple gravity by Alar and Juri Toomre in 1972 (ApJ 178, p. 623). The Toomres ran 3-body code to simulate galactic mergers. The three bodies are two galactic potentials and one test particle that moves at the behe st of these combining potentials. In one simulation, it is possible to have multiple test particles. Each particle tests a different starting position. On the order of 100 test particles were thrown into these potential wells.

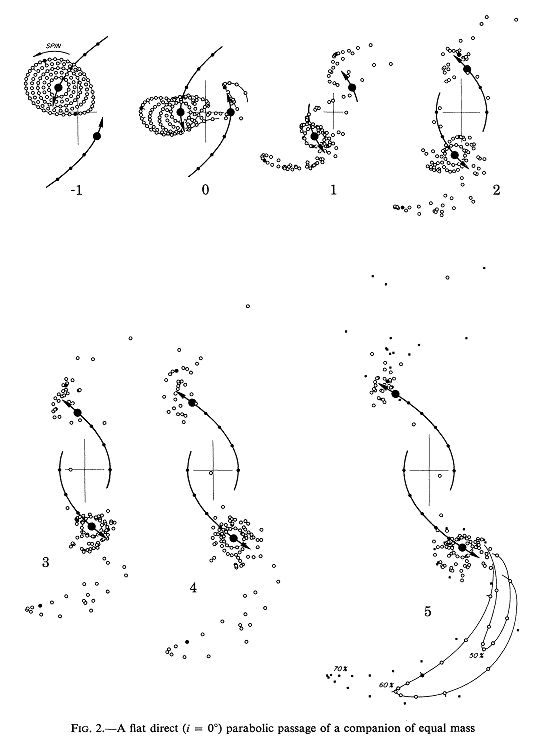
Figure 2: Evolution of interacting galaxies using 3-body method, note development of "tails" and "bridges" (Toomre & Toomre 1972)
The features that formed by running the model were arcs streaming out of the interacting galaxy as shown in figure 2. The Toomres called these arcs "tails". They also noticed similar features coming out the other side of galaxies which they called "anti-tails", but which are commonly called "bridges" because they appear to be material connecting two galaxies. The Toomres’ found that they could manipulate the size of these tidal features by altering the interaction geometry. There are four main parameters, the size of the orbit (or distance between the two galaxies), the ellipticity of the orbit, the inclination angle of each galaxy in relation to the orbital plane, and the amount which you rotate each galaxy about the axis perpendicular to the orbital plane, or argument of periapse. This geometry is shown in figure 3.
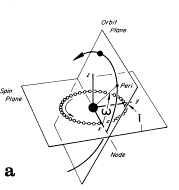
Figure 3: Encounter geometry, note "i" = inclination angle, "
w"=argument of periapse (Toomre & Toomre 1972)In general, the tail will be ejected in the plane of the galaxy, so if the galaxy is inclined to the orbital plane, the tail will come out at that inclination angle. As the inclination angle becomes greater (that is, as the galaxy’s plane become s more perpendicular to the orbital plane, assuming one starts with the galaxy rotating in the same direction as it is orbiting the other galaxy), the tail decreases in size. And then as that inclination angle becomes greater than perpendicular (the gala xy is rotating the direction opposite to the orbital direction), no tail is formed.
The other angular parameter with which one can fiddle, the argument of periapse, does not have as large an effect on the creation of the tidal features. The main effect is in viewing angle or the angle at which the tail appears to be in relationship t o the other galaxy’s tail. This is useful in the case where tails are coming out of both galaxies in an interacting system and one needs to have the two tails relate to one another at a certain angle. A much slighter effect is a widening of the tai l when the argument of periapse is increased.
It should be noted that the Toomres’ were not the first to use computers to simulate the gravitation effects on interacting galaxies. Nine years earlier, Pfleiderer (1963, Zs.f.Ap, 58, 12), a single grad student was unsuccessful in the formation o f tidal features because his galaxies moved past one another faster than they could have interacted.
Using all these tools, the Toomres’ were able to match the morphology (visual shape) of galaxies. They matched four systems: two with spirals and companion, Arp 295 and M51 (the "Whirlpool Galaxy"), and more typical early stage mergers, NGC 4038/ 9, "the Antennae", and NGC 4676, "the Mice".
At the time these matches were done, there was only good morphological data. Techniques for obtaining kinematics (velocity) data were confined to one-dimensional long slit spectra. These could only give kinematics in especially bright regions and the re only along a line. Today, Fabry-Perot interferometers can be used for bright optical sources while spectral line data collected by radio interferometers can be used for regions rich in neutral Hydrogen gas. Both of these techniques provide velocity i nformation for each point on an image. Thus, one can know the velocities at which points in the tail are moving relative to one another.
This information has made it possible to match more than morphology. My project stemmed from this desire to match n-body simulations to detailed observations. Several systems have already been matched using kinematics data including a rematch of NGC 4676 and NGC 7252. One might wonder at the need to rematch what the Toomres’ have already matched. It turned out that this additional exploration lead to the discovery that material in tails that is closer to the galaxy has a smaller apocenter than material farther out in the tail. This return of tail material to the merging body may cause fine gas structure in the resulting elliptical galaxy.
After matching such relatively simple interactions, there was a desire for something more challenging. In a survey of 14 interacting systems using the VLA, three particularly odd systems were found. Arp 299 was one of these. Using optical images, this galaxy looks like a relatively normal interacting system, with one galaxy producing a tail. But, when the VLA gas data was laid over the optical, the gas tail appeared separate from the optical. Reasons for this were guessed at: A) A superwind, created by the outflow from the numerous supernovae ignited by the galactic interaction could have created a hot, gaseous medium that would ram pressure strip the gas out of the tail, leaving the stars as an optical remnant. While this seems reasonable, the two tails seem like fully formed tidal features, each having been created on it’s own. This leads to a second possibility, B) The two tails are actually one very wide tail, that appears to be two because of projection effects. In this case, an explanation for the separation of materials needs to be found. In the Toomres’ model, outer rings of test particles begin the formation of the tail, followed by inner rings of test particles. Thus, the outside parts of tails are composed of the material from the outside of a galaxy while the inside of tails is from further in the galaxy. In the disk of spiral galaxies, optical surface brightness falls off exponentially, while the gas density falls off at a much less precipitous rate. Combining these two observations, it seems plausible that the outer part of a tail would be composed of primarily gas while the inner part would have a higher optical content. Then, if the galaxy were oriented towards us just right, we would see this disparity between tails.
It was this second possibility that led to my investigation of n-body simulations. What needed to be determined was whether or not just gravity could create a wide tail with different makeups at different locations. To do this, we first needed to run gravitational n-body simulations. The code that we used was created by Josh Barnes and uses a tree as a data structure to hold the particles that make up the galaxy. With this method, it is possible to quickly run a true n-body simulation. What separates an n-body simulation from a three-body simulation is the changing of potentials. In a three-body simulation, the potentials of the two massive bodies remain constant, while the third particle is effected by the changing summation of these 2 constant potentials. But, in an n-body, the potential energy contours are recalculated with each iteration based on the location of all n particles. The n-body method is better able to model the intricate gravitational effects than 3-body simulations.
The first step in running any simulation is to narrow parameter space by making assumptions based on observations. In our case, we knew that one of the galaxies did not create a tail. From the Toomres’, we know that this galaxy must be spinning with a retrograde orientation or be perpendicular to the orbital plane. A couple of initial attempts showed that the perpendicular orientation produced the proper morphology. The separation of the galaxies at periapse also needed to be determined. At too great a distance the galaxies would barely interact, too close and the interaction would happen too quickly producing an undersized tail. One-half of a scale unit was determined to be the proper distance. The remaining parameter to be manipulated was the angle at which the tail-forming galaxy should be to the orbital plane. This parameter could not be so easily determined. The tails formed by almost every inclination angle, except for extreme values (i > 50š), formed a tail with approximately the same morphology. fairly intense investigation of various inclination angles paired with various arguments of periapse did not produce significant variation. The most important piece of information found in this trade study was that none of the orbit al parameters created a wide tail. This finding is not yet a conclusion, though. The galaxy models that we were using contained hollow centers. It may be that these centers are what creates the tail width. The piece of evidence supporting this is Figu re 4 which is a much larger simulation that includes the central disk particles which were left out of the simulations I ran this summer. The large particles represent those from the outer half (?) of the disk, while the small particles are those from th e center of the disk. The greater tail width and separation of inner and outer disk particles is noticeable. Thus, a larger simulation needs to be run.
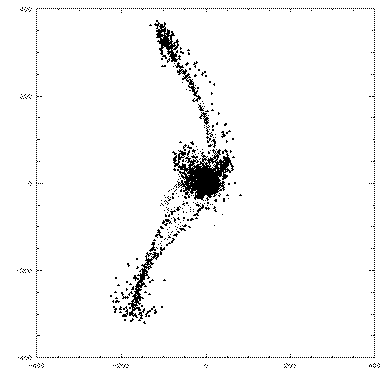
Figure 4: 64K particle Simulation. Small particles are from inside of disk, large from outer portion
If a larger simulation is not successful, there is another possibility for modeling Arp 299. Many disk galaxies that have been observed have a warp, meaning that a given ring of particles has a different inclination than more inner rings, and as a result is projected onto a different plane. While doing these simulations, we came to realize that a number of the 14 tailed systems had much less drastic bifurcated or parallel features, and that this might be a common phenomena. It seems plausible tha t a warp would cause a split tail, each component having a slightly different observable make up.
The viewing of these 6 dimensional simulations (3 spatial and 3 velocity components) is not a trivial matter. A program to do this viewing had been created prior to my arrival at NRAO, but its controls were cumbersome. To alleviate this problem, I a dded a graphical user interface to control the rotation, scaling, and other properties of the model. The experience in graphical user interface programming was invaluable.
The modeling of interacting galaxies has advanced since the days of Toomre and Toomre. Now we can examine kinematics data rather than just morphological and make more accurate models. We have also found out details about the process of galactic inter action which are critical to our understanding of the evolution of all types of galaxies.