MASS ESTIMATES OF TIDAL DWARF GALAXIES IN N-BODY SIMULATIONS OF INTERACTING DISK GALAXIES

Megan Kohring, University of Virginia

John Hibbard, National Radio Astronomy Observatory

Josh Barnes, Institute for Astronomy

ABSTRACT

Theoretical work (Barnes & Hernquist, 1992) suggests that dwarf galaxies may form within the tidal tails of interacting disk galaxies. Recent observational work purports to identify several so-called "Tidal Dwarf Galaxies" (TDGs) within tidal debris. However, the observational evidence that these TDGs are distinct, dynamical entities is circumstantial or non-existent. N-body simulations of colliding disk galaxies were run and gravitationally bound clumps were identified in the tidal tails. The N-body results were converted to simulated observations (moment maps) and "observable" quantities such as half-light radius, surface brightness and velocity dispersion were extracted from the clumps. From these, the "observed" mass (M_obs) and mass-to-light ratio (M/L)_obs can be determined, and compared to the true mass (M_true) and true mass-to-light ratio (M/L)_true of the clumps. We find that the locations of bound clumps in tidal tails often do not correspond to projected density peaks in the moment maps, so simulated observations do not recover the true properties of these regions.

N-BODY SIMULATIONS

Josh Barnes' Zeno software is a self-consistent N-body simulation package available for download at www.ifa.hawaii.edu/~barnes/treecode/treeguide.html Zeno simulates encounters of equal-mass disk galaxies using standard bulge-disk-halo models (for details, see Barnes, J.E. 1992). We ran two simulations with the parameters shown in Table 1.

Table 1. Parameters of galaxy models used in N-body simulations. N is the total number of particles in the simulation; N_bulge, N_disk, and N_halo are the number of particles in each bulge, disk and halo, respectively; N_tot is the total number of particles in each galaxy; M_bulge, M_disk, and M_halo are the masses of the bulge, disk and halo, respectively; and M_tot is the total mass of each galaxy.

GRIDDING THE DATA AND CALCULATING MOMENT MAPS

In order to turn our N-body data into simulated observations, we grid the data in the x-, y-, and vz-dimensions and compute moment maps using IDL. If i,j, and k represent the indices of the x-, y-, and vz-dimensions, respectively, N_ijk is the number of particles in pixel i,j,k of the grid, and V_k is the velocity of the k^th channel, then we can calculate moment maps using the following formulae:

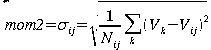
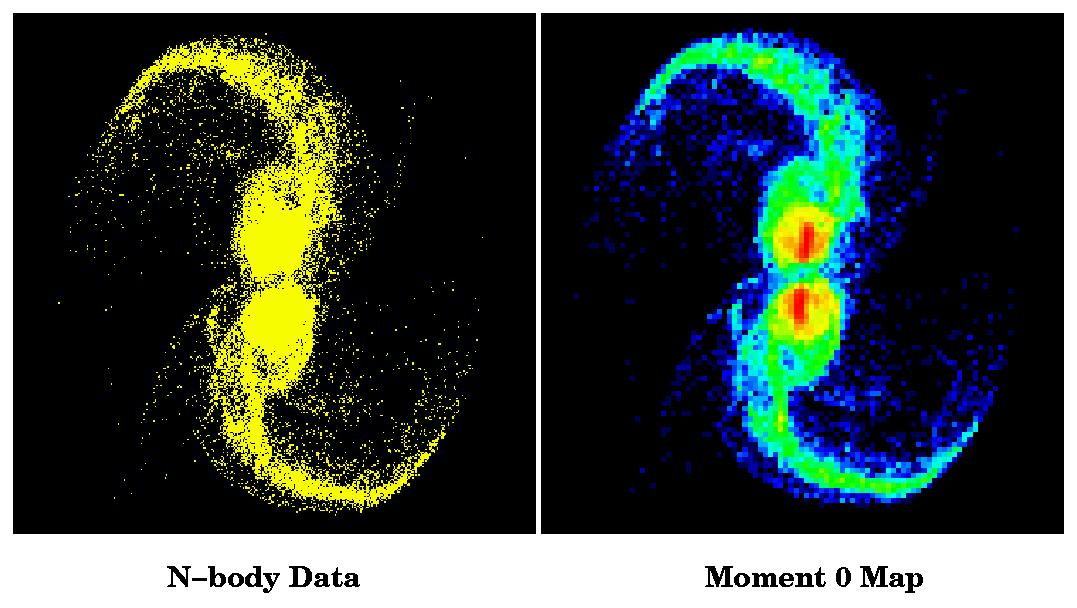
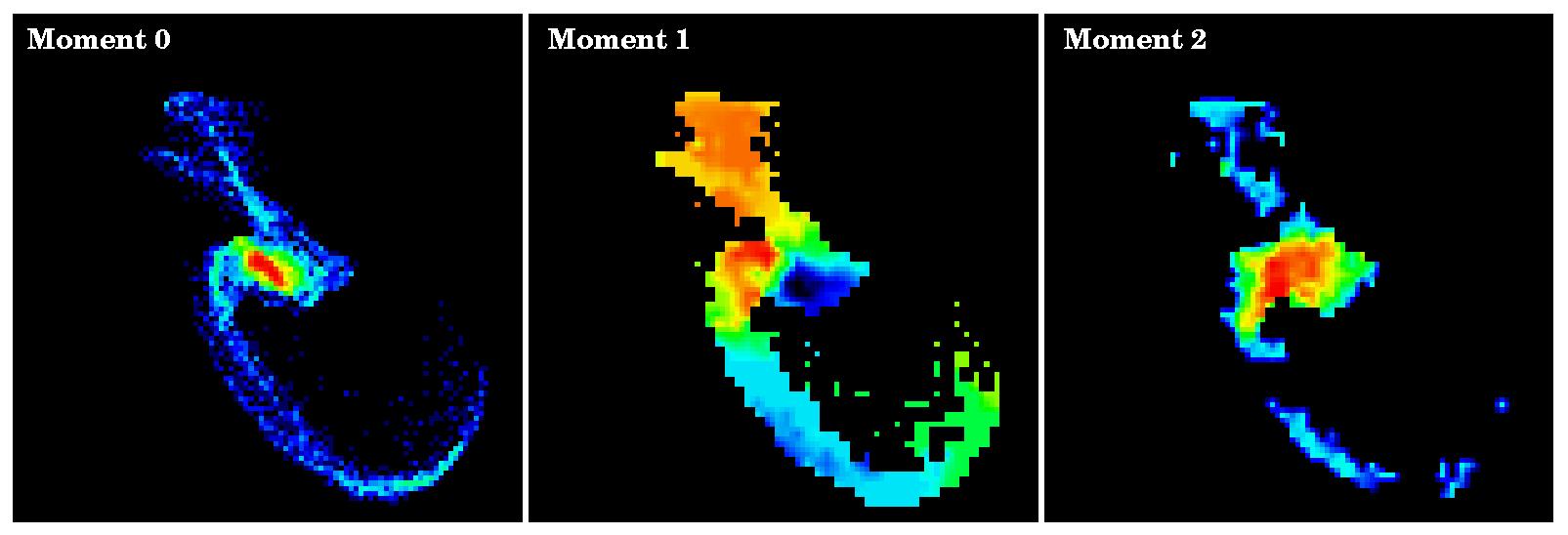
Mom0 is an integrated "intensity", or the number of particles in each pixel of the grid. Mom1 is an intensity-weighted velocity, and mom2 is an intensity-weighted velocity dispersion. In Figure 1 we show a comparison between the N-body data of our N=139264 simulation and the corresponding mom0 map, and in Figure 2 we show the mom0,1,2 maps for our N=69632 simulation.

Figure 1. N-body data and corresponding mom0 map for N=139264 model

Figure 1. Mom012 maps for N=69632 model

IDENTIFYING GRAVITATIONALLY BOUND REGIONS

Barnes' dwarf-finding procedure in Zeno utilizes a friends-of-friends algorithm which identifies bound regions in the tidal tails. We only consider 'virialized' regions with T/U < -0.4, where T is kinetic energy and U is potential energy. The result of the dwarf-finding procedure is shown in Table 2.

Table 2. Characteristics of 11 clumps found by Zeno. N is the number of particles in each clump; Mass is the mass of the clump for a Milky Way progenitor in solar units; x, y, and z are the coordinates of each clump; R_m/R_t is the mean radius divided by the tidal radius; if R_m/R_t < 1, the dwarf is expected to lose mass to the parent body as it orbits.

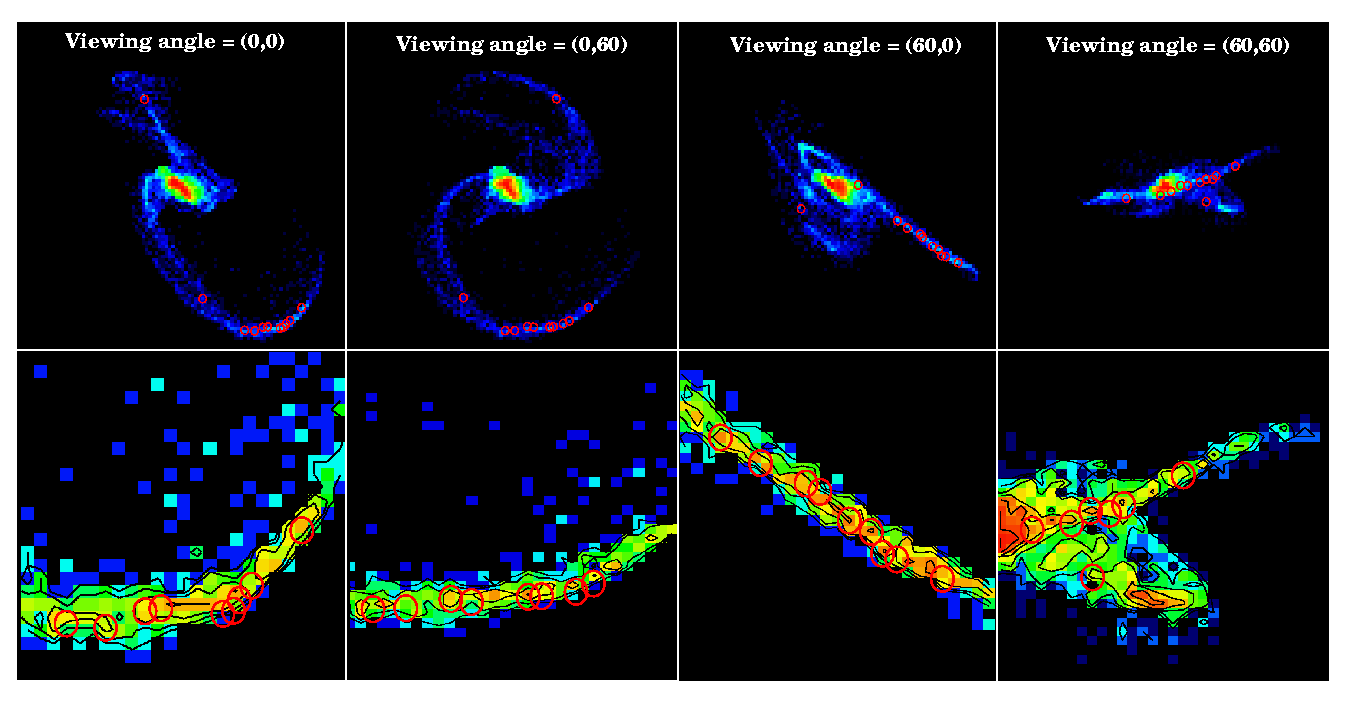
The locations of these 11 clumps are plotted on the mom0 map for our N=69632 simulation in Figure 3 for 2 different viewing angles, corresponding to rotations about the x- and y-axes, respectively (top). Also shown is a close-up contour map of the southern tidal tail at both viewing angles (bottom).

Figure 3. 11 clumps identified by Zeno dwarf-finding algorithm.

OBSERVATIONALLY DERIVED MASS ESTIMATES

From the virial theorem we can derive the virial mass of a bound object in a tidal tail:

where G is the Gravitational constant, â is the 1-dimensional velocity dispersion given by mom2 at the location of a bound region, a is a geometric factor (for a uniform density sphere, a=2.74), and r_1/2 is the half-light radius, obtained from fitting a Gaussian profile to the location of the clump in the mom0 map. (Binney & Tremaine, 1987)

The observed mass-to-light ratio (M/L)_obs of the clump is given by:

where G, â, and r_1/2 are the same as above and I₀ is the central surface brightness of the clump. (Richstone & Tremaine, 1986)

NOTE: we fit Gaussians to the known locations of bound regions regardless of whether there is a density peak in the mom0 map or not; this is different from how observers identify TDG candidates.

RESULTS & CONCLUSIONS

We find that the locations of some bound clumps in tidal tails do not correspond to density peaks in the mom0 maps so a Gaussian fit is not possible. In the regions that do correspond to density peaks, the estimations of r_1/2 and I₀ are too large, which leads to an estimate of M_vir that is orders of magnitude too large. This is most likely due to tidal material that is projected near the clumps but not bound to them. Thus, the true properties of bound regions are not recovered by simulated observations. Running higher-N simulations may help to resolve the TDGs in the tidal tails.

REFERENCES

Barnes, J.E. 1992, ApJ, 393, 484

Barnes, J.E., & Hernquist, L. 1992, Nature, 360, 715

Binney, J., & Tremaine, S. 1987, "Galactic Dynamics", (Princeton: Princeton University Press).

Richstone, D. and Tremaine, S. 1986, AJ, 92, 72