Geometric algebra is a mathematical system that extends traditional scalar algebra to higher dimensional constructs, such as vectors and directed plane segments, using an operation known as the Clifford product. Concepts from traditional vector algebra such as the cross product are defined in a manner that is extensible to higher dimensions, providing insight into geometrical relationships that renders awkward conventions such as the right-hand-rule for curls and cross-products unnecessary. It also provides a concrete interpretation for previously abstract ideas like the imaginary unit in complex analysis.
Geometric algebra has been found especially well suited to relativistic field theory in four-dimensional spacetime (as described in my book, Relativistic Field Theory for Microwave Engineers) and its proponents claim it has the potential to generalize and improve upon other mathematical formalisms as well, unifying virtually all physical theories and their associated mathematical techniques under one very flexible language.
While I agree with this ambition in general, I believe its advocates make the mistake of jumping too quickly into highly specialized disciplines such as quantum physics and general relativity. While it is good to know that each of these important subjects can be covered by the geometric algebra toolset, true adoption as the standard language for mathematical physics must start at a much more basic level. Preferably, in my view, it should be introduced to students as soon as they are prepared to advance beyond purely scalar mathematics and begin to talk about higher-dimensional objects like vectors.
The following is an attempt to summarize the rules of geometric algebra in that context, using three-dimensional space as a baseline.
Geometric algebra is coordinate-free, in that fundamental expressions can be written in a general form that does not depend on the particular coordinate system used. Nevertheless, it is useful to be able to reference a standard vector basis so that the meaning of various operations can be explored in familiar terms when needed.
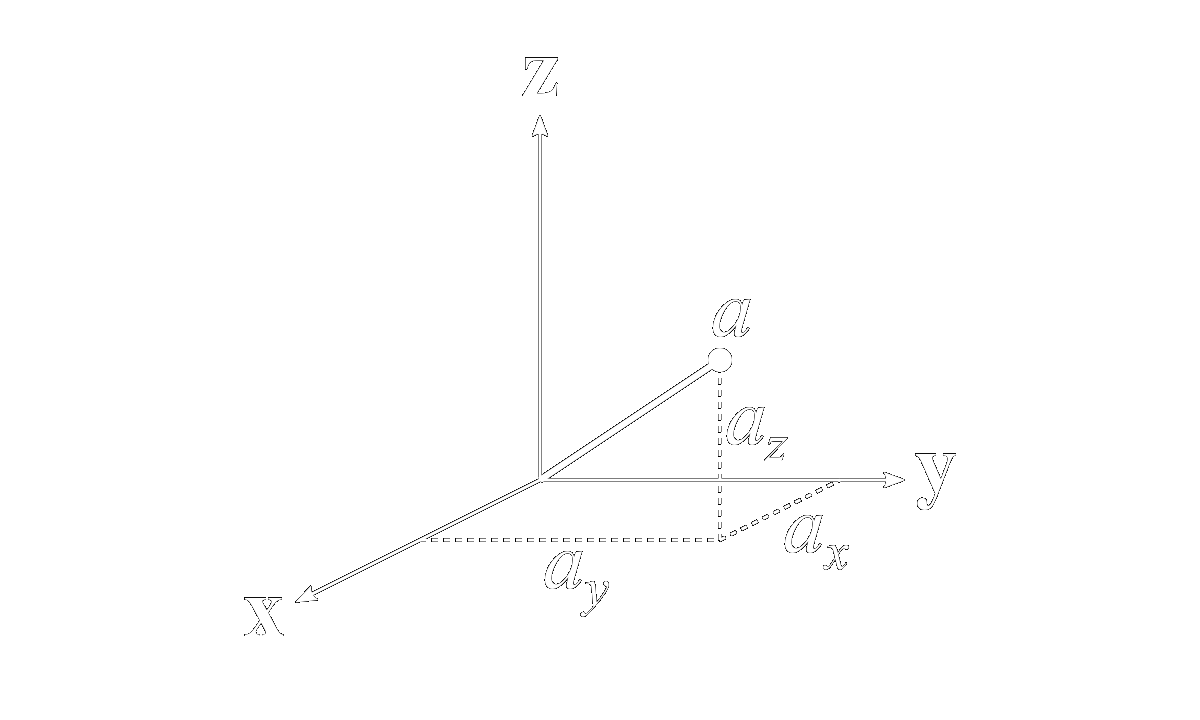
For three-dimensional geometry, we shall first use the standard Cartesian axes, \(\mathbf{x}\), \(\mathbf{y}\), and \(\mathbf{z}\), as our basis.

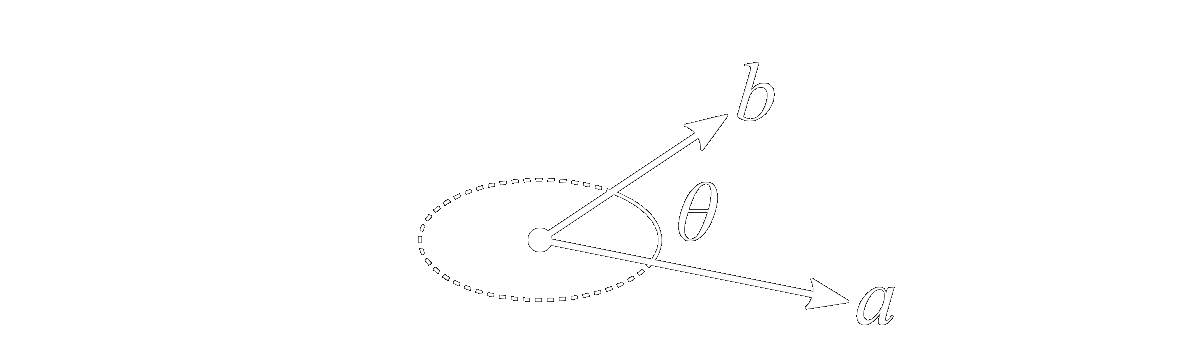
Thus, any vector \(a\) may be written as the sum of components along these directions, \[ a = a_x\mathbf{x}+a_y\mathbf{y}+a_z\mathbf{z} \] where \(\mathbf{x}\), \(\mathbf{y}\), and \(\mathbf{z}\) are unit vectors, \[ |\mathbf{x}|^2 = |\mathbf{y}|^2 = |\mathbf{z}|^2 = 1 \] It should be understood that the underlying operations performed upon such vectors transcend any particular coordinate representation. For example, the dot product of vectors \(a\) and \(b\) has the following form in Cartesian coordinates, \[ a\cdot b = a_xb_x+a_yb_y+a_zb_z \] and has different forms in cylindrical and spherical coordinates, but the geometric interpretation of the dot product in all three cases is the same, illustrated graphically below,
Typically, at this point in conventional vector analysis, we would introduce the cross product, yielding a third vector which is perpendicular to the other two. But there are several shortcomings to this approach.
For one, while the meaning of the dot product is unambiguous for vectors having any number of dimensions (e.g. two dimensions, three dimensions, four dimensions, etc.), the cross product can only be defined in three-dimensional space. One cannot, in general, define a third vector perpendicular to two others in two-dimensional space, and in four-dimensional space there are an infinite number of vectors that satisfy this condition.
The second issue with cross-products is their dependence on the so-called right-hand-rule, an awkward convention needed to define the orientation of the resultant vector relative to the other two. This convention is ultimately linked to the handedness of the coordinate system, and is necessary because cross-product vectors are what are known as axial vectors instead of the more typical polar vectors.
While we need not go into detail what is meant by these terms, I would argue like most proponents of geometric algebra that they arise because the outcome of an outer product of two vectors should not really be a vector at all, but rather a directed plane segment coincident with the two input vectors. (Consider the fact that the units associated with the product of two length vectors should be an area, not another length.) This is the result returned by the wedge product,
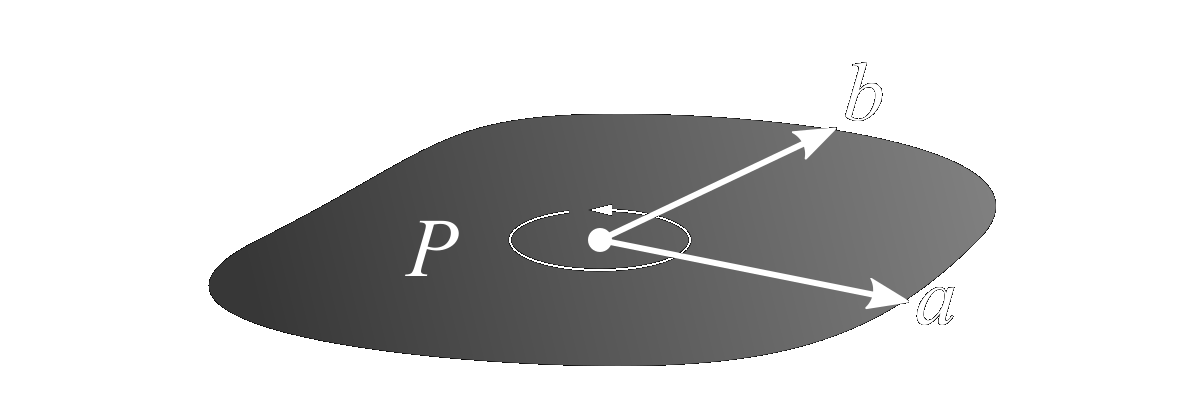
The object \(P\) is known as a bivector, and represents a directed plane segment in the same way that vectors \(a\) and \(b\) represent directed line segments. The traditional cross product would be the vector normal to this surface and given by the right-hand-rule. The orientation in this case need not reference the right-hand-rule, and is instead given by the direction of \(a\) sweeping toward \(b\).
The area of the planar patch defined by the bivector \(P\) is given by its magnitude, which is the area the parallelogram having edges \(a\) and \(b\), \[ \text{area}=|P|=|a||b|\sin\theta \] Importantly, the bivector does not encode the shape of the planar patch, only its attitude in space (the plane containing both \(a\) and \(b\)), its orientation (in the direction of \(a\) toward \(b\)), and its area. Thus, while the area is equivalent to that of the parallelogram described above, that shape itself is not implied by the bivector.
Scalars are called grade-0 objects, while vectors are grade-1, and bivectors are grade-2. A grade-3 object can be obtained by taking the wedge product again with a third vector, \(c\), \[ V = P\wedge c = a\wedge b\wedge c \] The trivector, \(V\), represents an oriented solid swept out by \(a\), \(b\), and \(c\), and has volume equal to that of the parallelepiped having these three vectors as its edges,
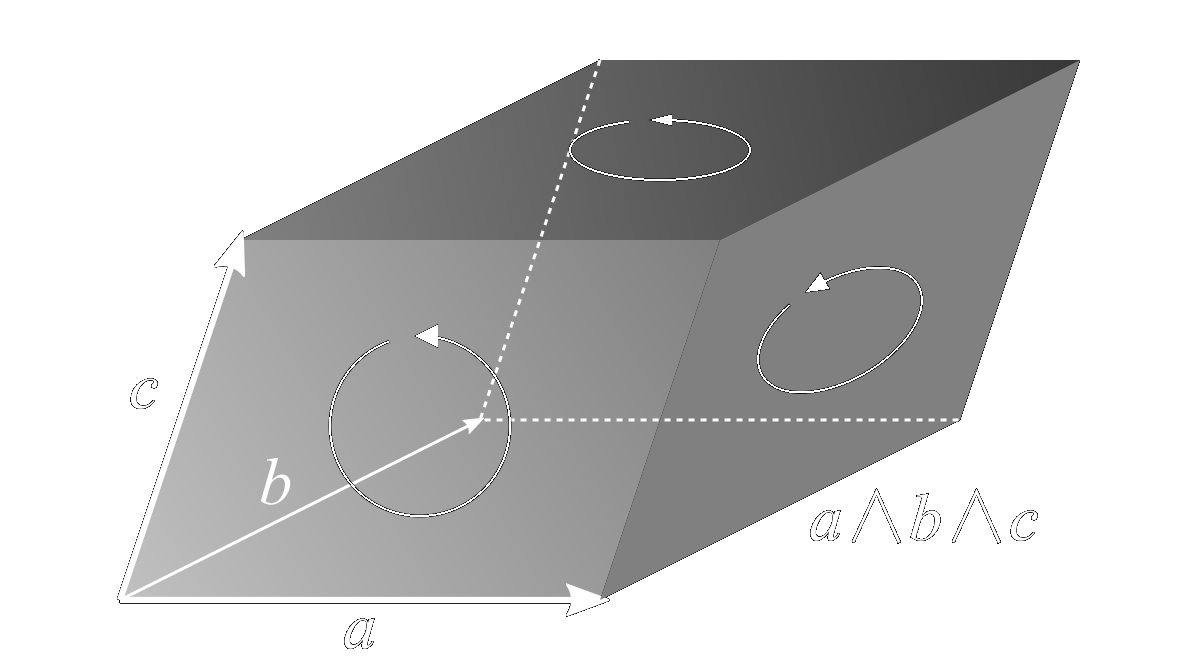
Note that if any of \(a\), \(b\), and \(c\) are colinear, then the volume and its associated trivector are zero. By extension, it is not possible to define a grade-4 object in three-dimensional space, because no four vectors can be linearly independent.
Finally, because of the orientation inherited from the sequence of vector operands, the wedge product is anticommutative, \[ a\wedge b = -b\wedge a \] This is in contrast with the dot product which is commutative, \[ a\cdot b = b\cdot a \] We may also note that he wedge product is associative, \[ a\wedge(b\wedge c) = (a\wedge b)\wedge c = a\wedge b\wedge c \] while the dot product is not.
We are now ready to define the Clifford product, also called the geometric product, a key operation in geometric algebra. Written simply as the juxtaposition \(ab\), it is the sum of the dot and wedge products of its operands, \[ ab = a\cdot b+a\wedge b \] But what does this represent? The dot product \((a\cdot b)\) is a scalar and the wedge product \((a\wedge b)\) is a bivector. How can such things be added? For our present purposes, the summation here means nothing more than that we have grouped the scalar and bivector quantities together into a mixed-grade product called a multivector, in the same way that real and imaginary parts are combined to create a complex number.
What is most critical is that the geometric product as a whole is associative, \[ a(bc) = (ab)c = abc \] and it also encodes enough information in its output to be invertible, \[ \text{if}\quad ab=c\quad\text{then}\quad b = a^{-1}c \] Neither the dot product nor the wedge product (nor the cross product) can be inverted in this way; they do not embed enough information in their result. The geometric inverse \(a^{-1}\) is another vector colinear with \(a\) but having the inverse of its magnitude, \[ a^{-1} = \frac{a}{a^2} \] where the denominator, the geometric product of \(a\) with itself, is by necessity a scalar, \[ a^2 = aa = a\cdot a+a\wedge a = |a|^2+0 = |a|^2 \] We may substitute this form back into the expression for \(b\) to verify that it functions as a multiplicative inverse, \[ b = a^{-1}c = \left(\frac{a}{a^2}\right)(ab) = \frac{a^2}{a^2}b = b \] Note that since the geometric product is defined as the sum of the dot product (a commutative form) and the wedge product (an anticommutative form), we may write these latter two products as the symmetric and antisymetric parts of the geometric product, \[ a\cdot b = \tfrac{1}{2}(ab+ba) \] \[ a\wedge b = \tfrac{1}{2}(ab-ba) \]
Since the basis vectors are orthogonal, their geometric product is equal to the dot product if the two operands are the same, and to the wedge product otherwise, e.g. \[ \mathbf{x}\mathbf{x} = \mathbf{x}\cdot\mathbf{x} = \mathbf{x}^2 = 1 \] \[ \mathbf{x}\mathbf{y} = \mathbf{x}\wedge\mathbf{y} = -\mathbf{y}\wedge\mathbf{x} = -\mathbf{y}\mathbf{x} \]
The single-grade elements of any multivector (namely scalars, vectors, bivectors, or trivectors) are called blades. More specifically, a grade-\(k\) object is also called a \(k\)-blade. The \(k\)-blade part of a general multivector, \(\mathcal{M}\), may be written \(\langle\mathcal{M}\rangle_k\). Thus, the multivector itself is simply the sum of its blades, \[ \mathcal{M} = \sum_{k=0}^3\langle\mathcal{M}\rangle_k \] The grade-0 (scalar) part of \(\mathcal{M}\) is sometimes abbreviated \(\langle\mathcal{M}\rangle\), without the subscript.
The geometric product, defined above only for vectors, can be generalized to blades as follows. For a \(k\)-blade \(K\) and an \(l\)-blade \(L\), \[ KL = \langle KL\rangle_{k+l}+\langle KL\rangle_{k+l-2}+\cdots+\langle KL\rangle_{|k-l|} \] In other words, the product is a multivector comprising blades that have grades ranging between the sum and difference of the grades of its operands, skipping by 2. We reserve the dot and wedge notation for the lowest and highest order terms in this summation, \[ K\cdot L = \langle KL\rangle_{|k-l|}\quad k\ge1,l\ge1 \] \[ K\wedge L = \langle KL\rangle_{k+l}\quad k\ge0,l\ge0 \] Note that we have excluded for the dot product the case where one of the operands is a scalar (grade 0). In such instances, the resulting summation only has one term, one blade, and that blade has the same grade as the other operand. Defining both the dot and wedge products here would double-count that term.
When one of the operands is a vector, \(a\), we have only the dot and wedge products resulting, \[ aK = a\cdot K+a\wedge K \] \[ Ka = K\cdot a+K\wedge a \] and furthermore, \[ a\cdot K = (-1)^{k+1}K\cdot a = \tfrac{1}{2}\left(aK+(-1)^{k+1}Ka\right) \] \[ a\wedge K = (-1)^kK\wedge a = \tfrac{1}{2}\left(aK+(-1)^kKa\right) \] Since the geometric product is both associative and distributive, products of general multivectors can be derived from the above rules by first breaking them down into a summation of their constituent blades.
We stated at the beginning that the three basis vectors were normalized to unit value, \[ \mathbf{x}^2 = \mathbf{y}^2 = \mathbf{z}^2 = 1 \] But what about the other blades formed from them? Consider, for example, the square of the bivector formed between the \(\mathbf{x}\) and \(\mathbf{y}\) axes, \[ (\mathbf{x}\wedge\mathbf{y})^2 = (\mathbf{x}\mathbf{y})^2 = \mathbf{x}\mathbf{y}\mathbf{x}\mathbf{y} = -\mathbf{x}\mathbf{y}^2\mathbf{x} = -\mathbf{x}^2 = -1 \] We find that the square norm of this bivector has a negative signature. The same holds true of the other Cartesian planes, \[ (\mathbf{xy})^2 = (\mathbf{yz})^2 = (\mathbf{zx})^2 = -1 \] Finally, let us consider the square norm of the unit three-volume, \[ (\mathbf{xyz})^2 = \mathbf{xyzxyz} = -\mathbf{xyzzyx} = -1 \]
While one may identify up to three, mutually independent, unit bivector planes, (\(\mathbf{xy}\), \(\mathbf{yz}\), and \(\mathbf{zx}\)), there is only one independent unit three-volume, or trivector, in three-dimensional space (all other trivectors simply being scalar multiples of it). We give this unit trivector the special symbol, \(i\), \[ i = \mathbf{xyz} \] This will typically be referred to as the unit pseudoscalar element, and can be identified with the imaginary unit in complex analysis. This is not only because \(i^2=-1\), but because it commutes with all other scalars, vectors, bivectors, and trivectors, just like any other scalar. The bivector planes also square to minus one as we have just shown, however they do not commute in geometric products with other elements in the same way that scalars and pseudoscalars do.
The subalgebra involving geometric products of only scalars and pseudoscalars (that is, excluding vectors and bivectors) exactly replicates complex analysis. This is but one simple example of how geometric algebra both contains and supercedes other familiar forms of mathematical analysis.
The complete algebraic domain of geometric algebra thus consists of the scalars, vectors, bivectors, and trivectors, \[ \lbrace 1\rbrace, \lbrace\mathbf{x},\mathbf{y},\mathbf{z}\rbrace, \lbrace\mathbf{xy},\mathbf{yz},\mathbf{zx}\rbrace, \lbrace\mathbf{xyz}\rbrace \] shown graphically below,
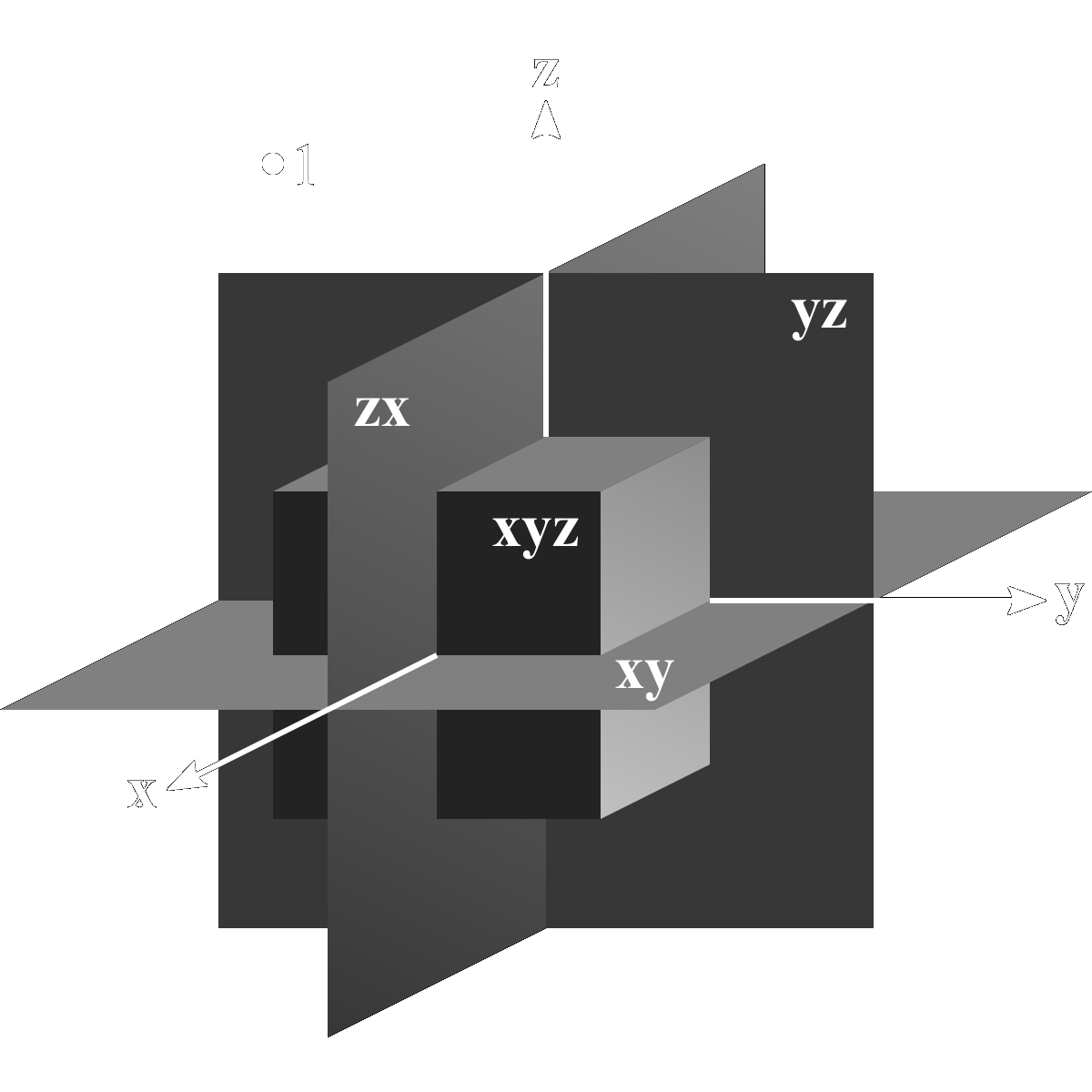
All quantities can be expressed as scalar multiples of this set and all operations performed on those quantities yield results within that set.
It can be shown that the bivectors are given by the products of vectors and the pseudoscalar. For example, \[ \mathbf{xy} = \mathbf{xyzz} = i\mathbf{z} \] Similarly, \[ \mathbf{yz} = i\mathbf{x} \] \[ \mathbf{zx} = i\mathbf{y} \] Therefore, the algebraic domain may also be written \[ \lbrace 1\rbrace, \lbrace\mathbf{x},\mathbf{y},\mathbf{z}\rbrace, \lbrace i\mathbf{x},i\mathbf{y},i\mathbf{z}\rbrace, \lbrace i\rbrace \] The bivectors \(i\mathbf{x}\), \(i\mathbf{y}\), and \(i\mathbf{z}\) are sometimes called pseudovectors in recognition of this form. Multiplication by the pseudoscalar \(i\) is a form of duality that has numerous applications in geometric algebra. It can be shown, for example, that the dot and wedge products are duals of each other, \[ i(\mathcal{M}\cdot a) = (i\mathcal{M})\wedge a \] \[ i(\mathcal{M}\wedge a) = (i\mathcal{M})\cdot a \]
The dot product is traditionally associated with geometric projection. Classically, the projection of vector \(a\) onto \(b\) is written \[ \text{proj}_ba = \frac{a\cdot b}{b\cdot b}b = (a\cdot b)\frac{b}{|b|^2} \] We may recognize the last term above as the formula for the inverse of \(b\) in geometric algebra. Thus, we can write \[ \text{proj}_ba = (a\cdot b)b^{-1} \] Moreover, the residual vector after projection, that vector which connects \(\text{proj}_ba\) back to \(a\), is called the rejection of \(a\) from \(b\), and is written using the wedge product, \[ \text{rej}_ba = (a\wedge b)b^{-1} \] This is illustrated below.
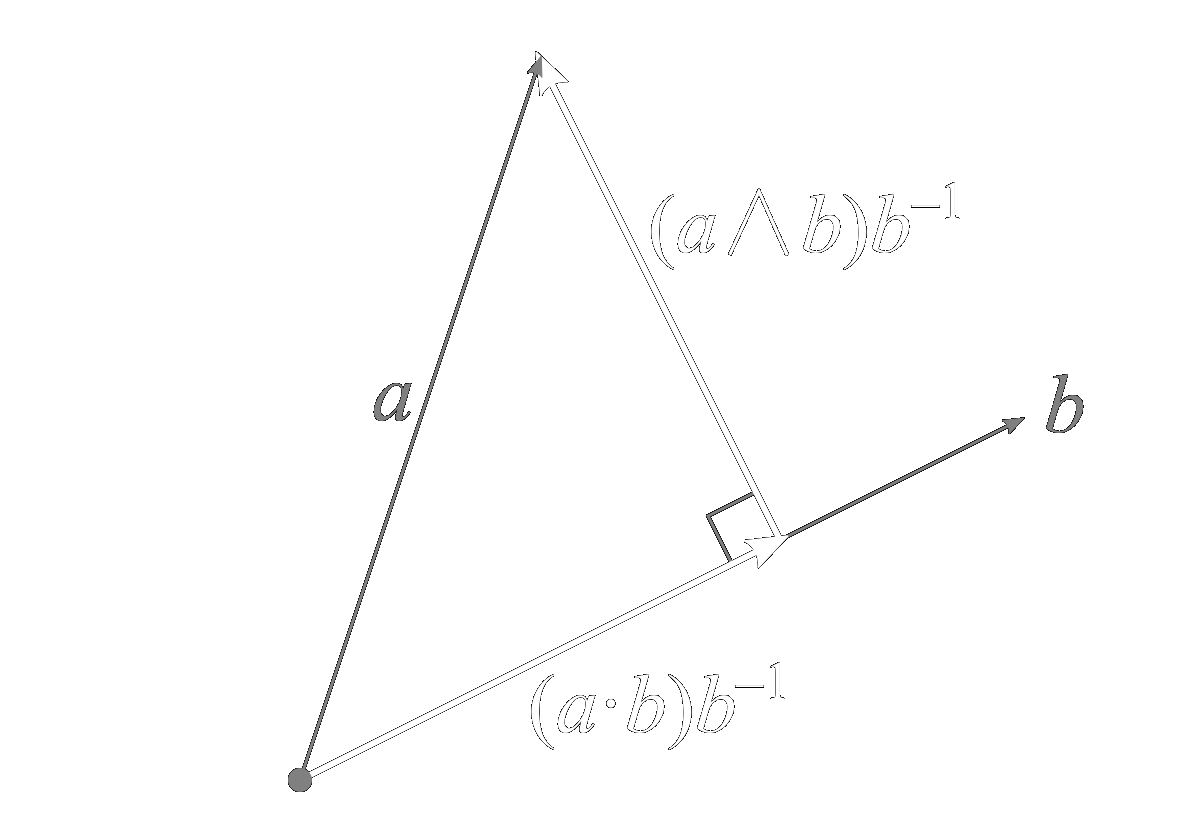
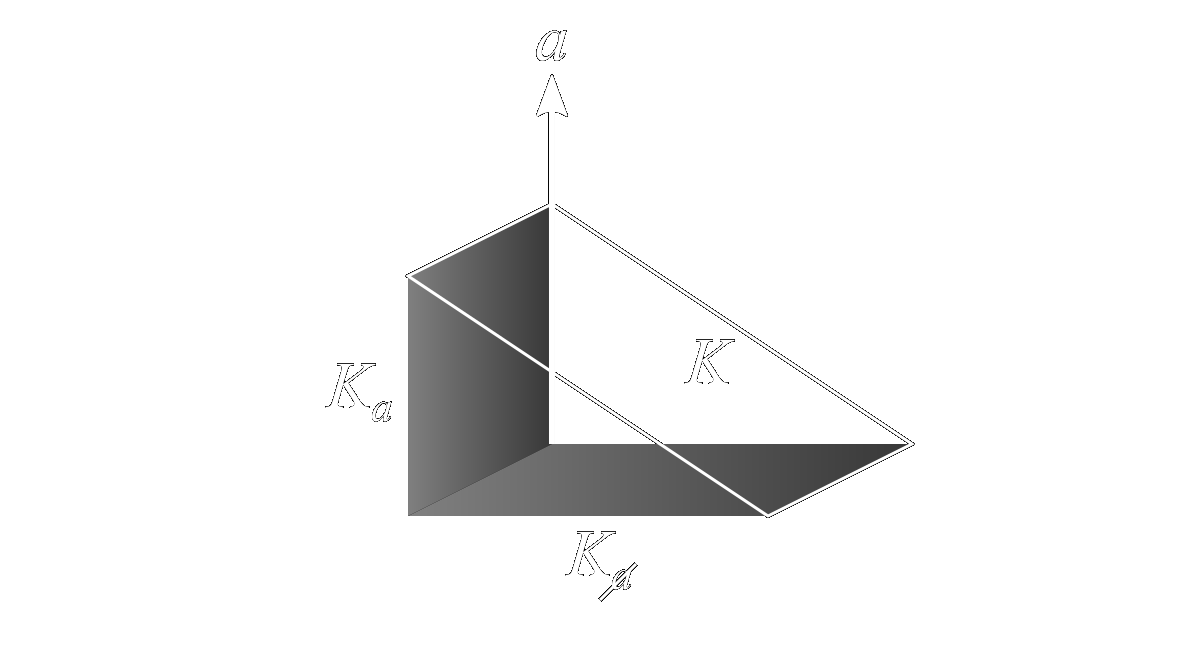
I like to abbreviate the projection and rejection formulas using subscripts of the new basis vector with and without a line through it, respecitvely, as follows, \[ a_b = \text{proj}_ba = (a\cdot b)b^{-1} \] \[ a_\cancel{b} = \text{rej}_ba = (a\wedge b)b^{-1} \] It thus follows that any vector is the sum of its projection onto and rejection from another vector, \[ a = a_b+a_\cancel{b} \] The beauty of geometric algebra is that these formulas work not only for vectors, but blades in general. For example, the projection and rejection of a vector \(a\) onto and from a plane \(K\) are given by \[ a_K = (a\cdot K)K^{-1} \] \[ a_\cancel{K} = (a\wedge K)K^{-1} \] where \[ K^{-1} = \frac{K}{K^2} \] This is illustrated below,
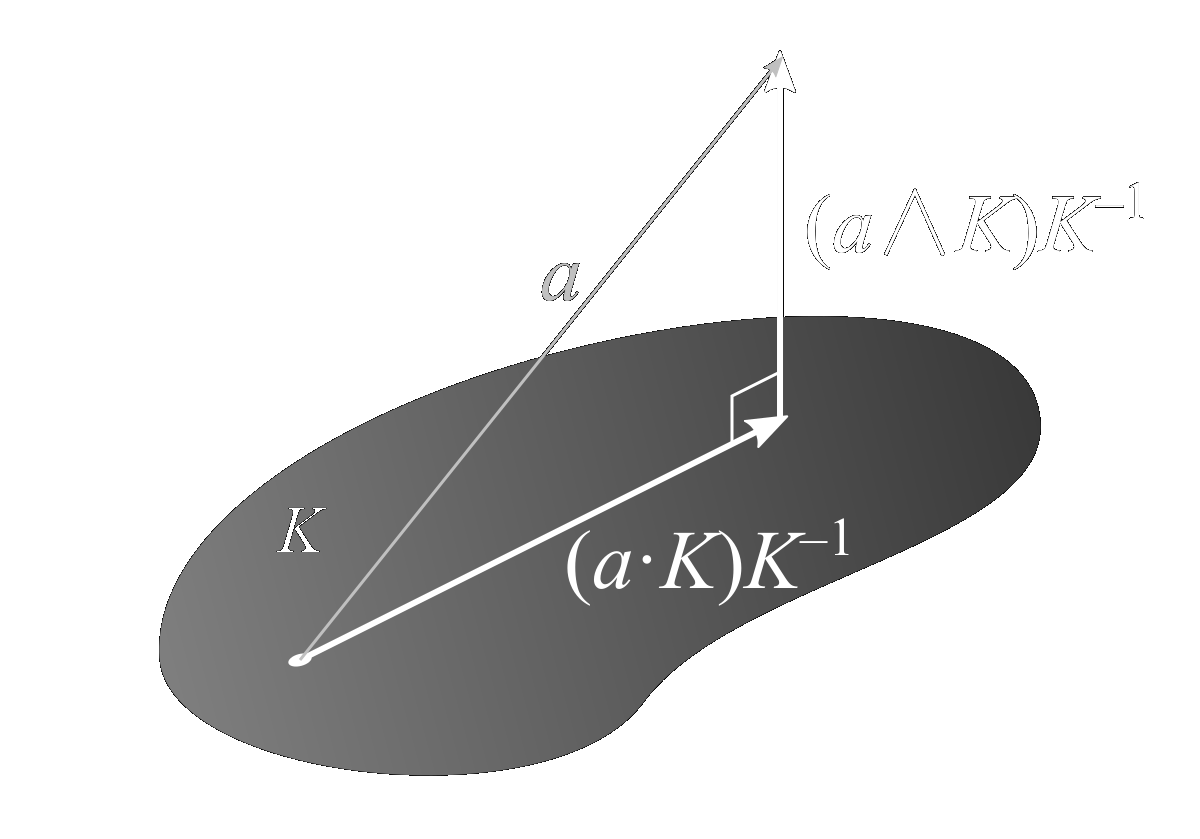
Recall that the Cartesian bivector planes are the duals of the vectors which serve as their surface normals, e.g. \(\mathbf{xy}=i\mathbf{z}\). This general trend holds for all bivectors and surface normals, not just those that align with the Caretsian axes. Consequently, the projection of a vector onto a plane is also the rejection from that plane's surface normal, which happens to be its dual. The overall conclusion is that the projection and rejection operations are duals of one another, \[ a_\cancel{K} = a_{iK} \]
As a final example, we consider the projection of a plane onto a vector, and its rejection there from,
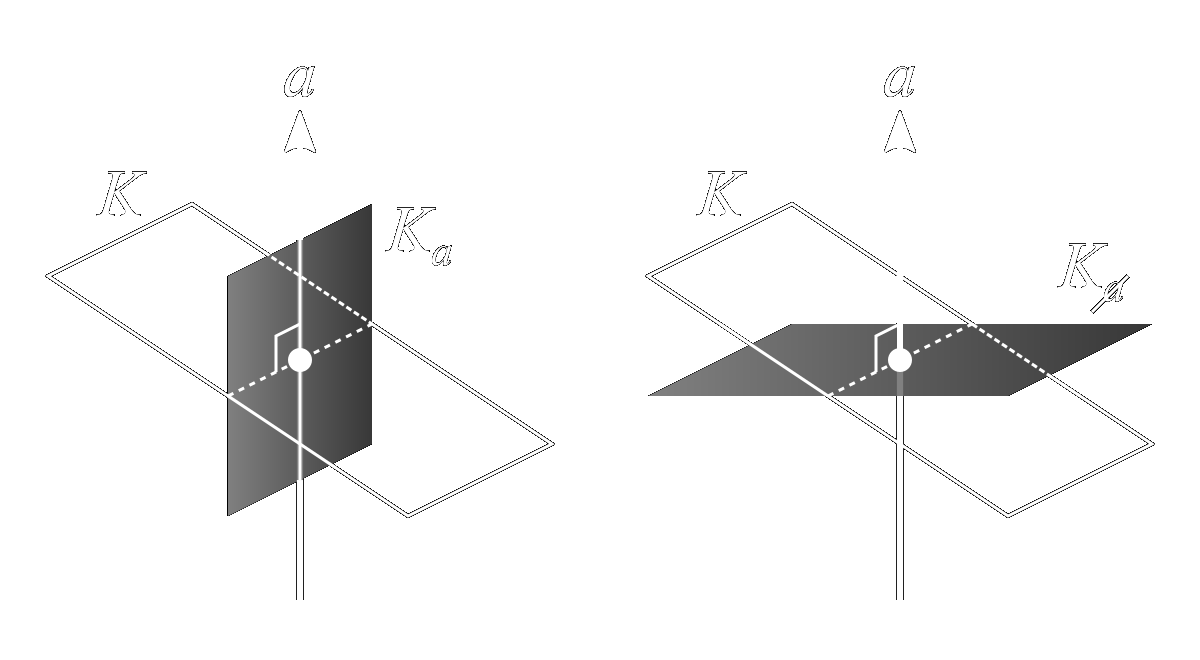
where \[ K_a = (K\cdot a)a^{-1} \] \[ K_\cancel{a} = (K\wedge a)a^{-1} \] Once again, the orignal plane \(K\) is the sum of its projection and rejection from the given vector
As an example of how simple geometric analyses can be using this toolset, we shall now derive some well-known results. Consider the triangle below formed by the arbitrary vectors \(a\), \(b\), and \(c\), subtended by the angles \(A\), \(B\), and \(C\).
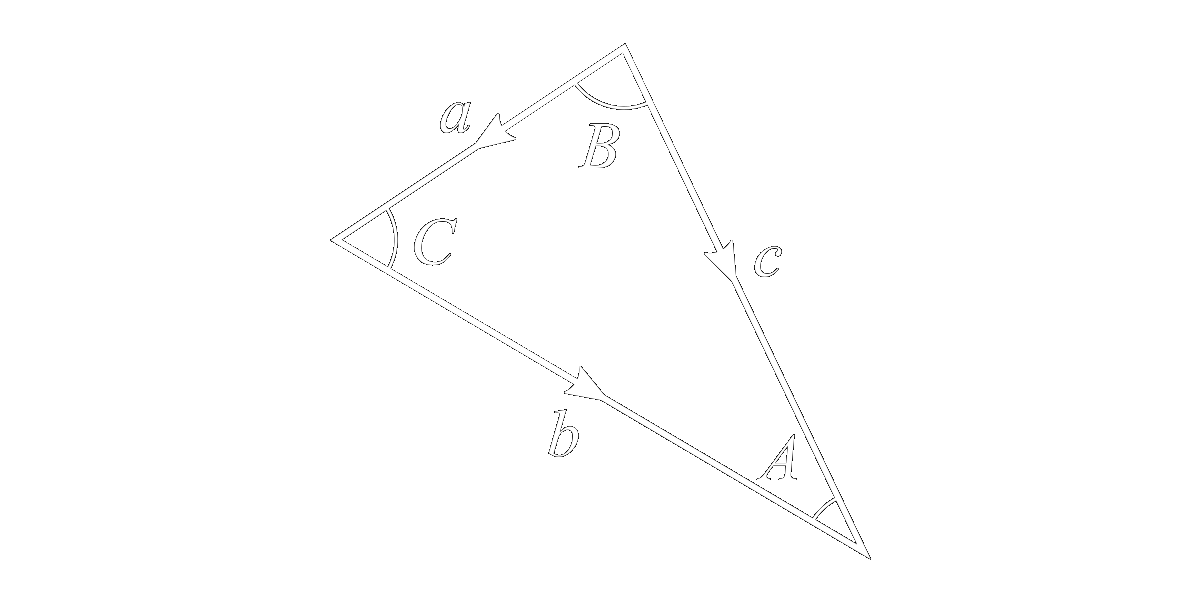
The vectors \(a\) and \(b\) are arranged head to tail and conjoined with \(c\), so that we may write \[ a + b = c \] Let us now take the wedge product of both sides with \(c\), \[ a\wedge c + b\wedge c = \cancel{c\wedge c} = 0 \] where we have indicated that the wedge product of \(c\) with itself vanishes. Therefore, \[ a\wedge c = c\wedge b \] \[ |a||c|\sin B = |c||b|\sin A \] \[ \frac{\sin A}{|a|} = \frac{\sin B}{|b|} \] which is the law of sines. We could have arrived at this result even more quickly by noticing that \(a\wedge c\) and \(c\wedge b\) sweep out the same bivector (or at least the same half-bivector, since the triangle is half of the relevant parallelogram in each case), allowing us to immediately write \(a\wedge c = c\wedge b\).
If instead we took the dot product of the original equation with \(c\), we would have
\[ a+b = c \] \[ a\cdot c + b\cdot c = c\cdot c = c^2 \] Then, substituting back in that \(c=a+b\), we have \[ a\cdot(a+b) + b\cdot(a+b) = c^2 \] \[ a^2+b^2+2a\cdot b = c^2 \] The angle \(C\) is subtended, not by the vectors \(a\) and \(b\), but rather by \(-a\) and \(b\). Therefore, \[ a^2+b^2-2|a||b|\cos C = c^2 \] which is the law of cosines.As a final example, consider the irregular polygon shown below. It has \(N\) vertices labeled \(p_1\) through \(p_N\) (plus a final vertex \(p_{N+1}\) that is concurrent with the first), and we have chosen an aribtrary point somewhere in the center, labeled \(c\).
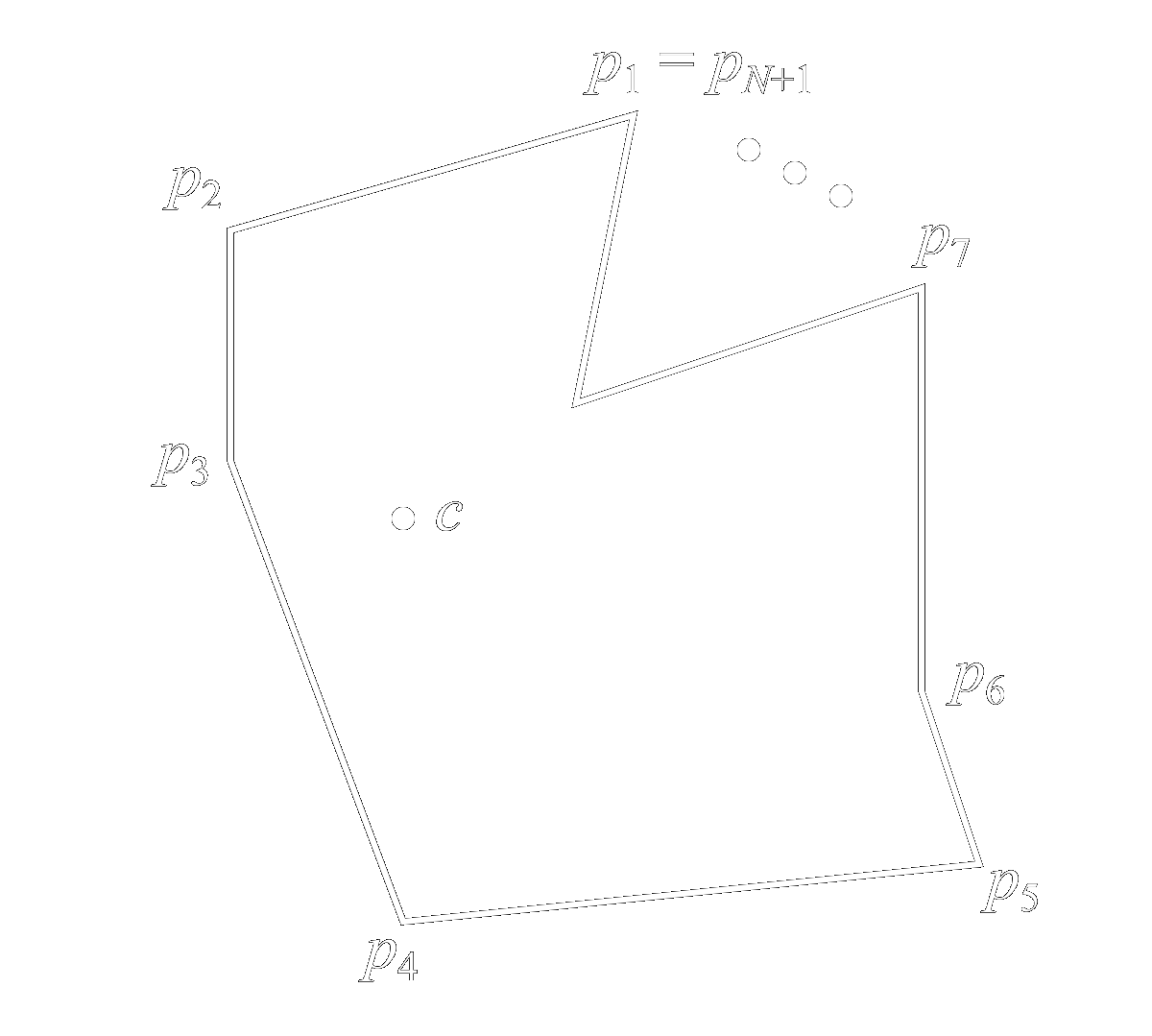
To calculate the area, let us divide the interior into triangles formed by adjacent vertices and the point \(c\). Each triangle may be considered half of the bivector parallelogram formed by the lines radiating from point \(c\) to the adjacent vertices, as shown.
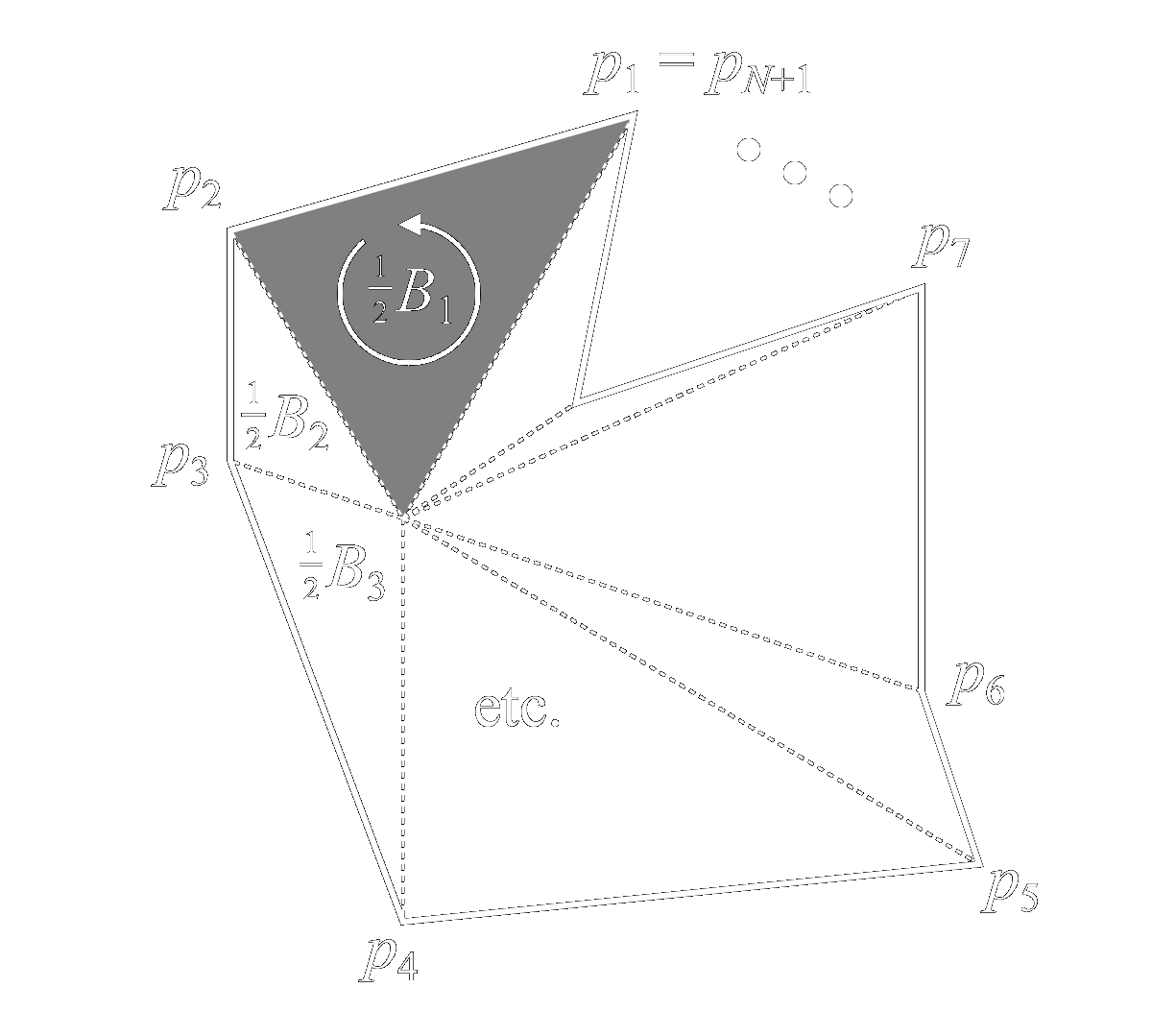
Note that there are a total of \(N\) such bivector patches. Bivector \(B_k\) is given by \[ B_k = \left(p_k-c\right)\wedge\left(p_{k+1}-c\right) \] \[ = p_k\wedge p_{k+1}-c\wedge\left(p_{k+1}-p_k\right)+\cancel{c\wedge c} \] The total area of the polygon, \(A\), is half the sum of all \(N\) bivectors, \[ A = \frac{1}{2}\sum_{k=1}^NB_k = \frac{1}{2}\sum_{k=1}^Np_k\wedge p_{k+1} - \frac{c}{2}\wedge\left(\sum_{k=1}^N\left(p_{k+1}-p_k\right)\right) \](More accurately, \(A\) is a bivector whose magnitude is equal to the area of the polygon.) Note that the final term in parentheses above is just a closed loop of vectors added head to tail, and thus sums to zero. Therefore, \[ A = \frac{1}{2}\sum_{k=1}^Np_k\wedge p_{k+1} \]
To put this in a more familiar form, we may expand the wedge product in the \(\mathbf{xy}\) bivector plane, \[ p_k\wedge p_{k+1} = \left(x_k\mathbf{x}+y_k\mathbf{y}\right)\wedge\left(x_{k+1}\mathbf{x}+y_{k+1}\mathbf{y}\right) = \mathbf{xy}\left(x_ky_{k+1}-x_{k+1}y_k\right) \] Therefore, \[ A = \frac{1}{2}\mathbf{xy}\sum_{k=1}^N\left(x_ky_{k+1}-x_{k+1}y_k\right) \] Excepting the bivector prefactor, \(\mathbf{xy}\), some may recognize this as the so-called Shoelace formula or surveyor's formula for the area of an irregular polygon given the coordinates of its vertices.
While this article has focused on geometric algebra in ordinary Euclidean space, the same general principles apply to non-Euclidean geometries and to higher dimensions as well. One of the most interesting applications of this concept is to electromagnetics under special relativity. For that, we construct a geometric algebra based on four-dimensional spacetime, where the basis vectors have the following normalization, or metric signature, \[ \mathbf{x}^2 = \mathbf{y}^2 = \mathbf{z}^2 = -(c\mathbf{t})^2 = \pm1 \] This construction is known as spacetime algebra . For more information, the reader is referred to my book, Relativistic Field Theory for Microwave Engineers:

Now available at BookBaby and Amazon.com.
Some useful identities are provided below to aid the reader in exploring the concepts of geometric algebra further.
In the identities that follow:
Commutation:
\[ \psi\mathcal{M} = \mathcal{M}\psi \] \[ i\mathcal{M} = \mathcal{M}i \] \[ a\cdot K = (-1)^{k+1}K\cdot a \] \[ a\wedge K = (-1)^kK\wedge a \]Trace:
\[ \langle\mathcal{MN}\rangle = \langle\mathcal{NM}\rangle \]Duality:
\[ i\langle\mathcal{M}\rangle_k = \langle i\mathcal{M}\rangle_{3-k} \] \[ a_\cancel{K} = a_{iK} \] \[ K_\cancel{a} = K_{ia}\quad k=1,2 \] \[ i(\mathcal{M}\cdot a) = (i\mathcal{M})\wedge a \] \[ i(\mathcal{M}\wedge a) = (i\mathcal{M})\cdot a \]Projection and Rejection:
\[ (\mathcal{M}+\mathcal{N})_K = \mathcal{M}_K + \mathcal{N}_K \] \[ (\mathcal{M}+\mathcal{N})_\cancel{K} = \mathcal{M}_\cancel{K} + \mathcal{N}_\cancel{K} \] \[ \mathcal{M} = \mathcal{M}_a + \mathcal{M}_\cancel{a} \] \[ a = a_K + a_\cancel{K} \] \[ a_b\cdot\mathcal{M}_b = a_b\cdot\mathcal{M} \] \[ a_b\cdot\mathcal{M}_\cancel{b} = 0 \] \[ a_\cancel{b}\cdot\mathcal{M}_b = (a\cdot\mathcal{M})_b \] \[ a_\cancel{b}\cdot\mathcal{M}_\cancel{b} = a\cdot\mathcal{M}_\cancel{b} \] \[ a_b\wedge\mathcal{M}_b = 0 \] \[ a_b\wedge\mathcal{M}_\cancel{b} = a_b\wedge\mathcal{M} \] \[ a_\cancel{b}\wedge\mathcal{M}_b = a\wedge\mathcal{M}_b \] \[ a_\cancel{b}\wedge\mathcal{M}_\cancel{b} = (a\wedge\mathcal{M})_\cancel{b} \] \[ a_b\mathcal{M}_b = a_b\cdot\mathcal{M} \] \[ a_b\mathcal{M}_\cancel{b} = a_b\wedge\mathcal{M} \] \[ a_b\mathcal{M} = a_b\cdot\mathcal{M}_b + a_b\wedge\mathcal{M}_\cancel{b} \] \[ a_{KL} = a_K + a_L\quad\text{if}\quad KL= K\wedge L \] \[ \left(\mathcal{M}_K\right)_L = \left(\mathcal{M}_L\right)_K\quad\text{if}\quad KL=K\wedge L \]Products:
\[ a\mathcal{M} = a\cdot\mathcal{M}+a\wedge\mathcal{M} \] \[ \mathcal{M}a = \mathcal{M}\cdot a+\mathcal{M}\wedge a \] \[ a\cdot K = \tfrac{1}{2}\left(aK+(-1)^{k+1}Ka\right) \] \[ a\wedge K = \tfrac{1}{2}\left(aK+(-1)^kKa\right) \] \[ K\cdot L = \langle KL\rangle_{|k-l|}\quad k,l\ge1 \] \[ K\wedge L = \langle KL\rangle_{k+l}\quad (k+l)\le4 \] \[ a\cdot(bc) = a\cdot(b\wedge c) = (a\cdot b)c - (a\cdot c)b \] \[ a\wedge(bc) = a(b\cdot c) + a\wedge b\wedge c \] \[ a(b\wedge c) = (a\cdot b)c - (a\cdot c)b + a\wedge b\wedge c \] \[ abc = (a\cdot b)c - (a\cdot c)b + (b\cdot c)a + a\wedge b\wedge c \] \[ a\cdot(b\cdot K) = -b\cdot(a\cdot K) = (K\cdot a)\cdot b \] \[ a\cdot(bK) = (a\cdot b)K - b(a\cdot K) \] \[ a\cdot(b\wedge K) = (a\cdot b)K - b\wedge(a\cdot K) \] \[ a\wedge(b\cdot K) = (a\cdot b)K - b\cdot(a\wedge K) \] \[ a\cdot(K\wedge L) = (a\cdot K)\wedge L+(-1)^kK\wedge(a\cdot L) \] \[ (a\wedge b)\cdot(c\wedge d) = (a\cdot d)(b\cdot c) - (a\cdot c)(b\cdot d) \] \[ a\cdot(b\wedge c\wedge d) = (a\cdot b)(c\wedge d) - (a\cdot c)(b\wedge d) + (a\cdot d)(b\wedge c) \]Degenerate Forms:
\[ \left(\mathcal{M}_K\right)_\cancel{K} = \left(\mathcal{M}_\cancel{K}\right)_K = 0 \] \[ (\mathcal{M}\cdot a)\cdot a = 0 \] \[ \mathcal{M}\wedge a\wedge a = 0 \] \[ (\mathcal{M}\cdot a)\wedge a = (\mathcal{M}\cdot a)a = (\mathcal{M}a)\wedge a \] \[ (\mathcal{M}\wedge a)\cdot a = (\mathcal{M}\wedge a)a = (\mathcal{M}a)\cdot a \] \[ K_i = K_\cancel{1} = K\quad k\ge 1 \] \[ K_\cancel{i} = K_1 = 0\quad k\ge 1 \]