


Next: 4.3 Model description
Up: 4 Model results
Previous: 4.1.6 Features that cannot be fitted well
4.2 Model parameters and confidence limits
The optimization problem is complicated, and estimates of some of the
parameters are strongly correlated. In addition, we do not know the
statistics (or even the rms level) of the ``noise'' a priori and we have
imposed additional constraints by our choice of fitting functions. The
 statistic is effective in optimizing the fit, but assessing
confidence limits (e.g. by a Bayesian analysis or using bootstrap
techniques) would be far from straightforward. We have instead adopted a
simple ad hoc procedure, by which we vary a single parameter until the
fractional increase in the
statistic is effective in optimizing the fit, but assessing
confidence limits (e.g. by a Bayesian analysis or using bootstrap
techniques) would be far from straightforward. We have instead adopted a
simple ad hoc procedure, by which we vary a single parameter until the
fractional increase in the  values for I or Q and U in
one of the inner, flaring or outer regions corresponds to the formal
99% confidence limit for independent Gaussian errors and the appropriate
number of degrees of freedom. Most parameters affect the fit
significantly only for part of the jet, or for a subset of the Stokes
parameters, so this approach is superior to one based on the total
values for I or Q and U in
one of the inner, flaring or outer regions corresponds to the formal
99% confidence limit for independent Gaussian errors and the appropriate
number of degrees of freedom. Most parameters affect the fit
significantly only for part of the jet, or for a subset of the Stokes
parameters, so this approach is superior to one based on the total
 . The estimates are qualitatively reasonable, in the sense that
varying a parameter by its assigned error leads to a visibly unacceptable
fit, and we believe that they give a good general impression of the range
of allowed models. The numerical confidence levels should not be taken
too seriously, however.
. The estimates are qualitatively reasonable, in the sense that
varying a parameter by its assigned error leads to a visibly unacceptable
fit, and we believe that they give a good general impression of the range
of allowed models. The numerical confidence levels should not be taken
too seriously, however.
Table 7:
Fitted parameters and error estimates.
| Quantity |
SSL |
Gauss |
| |
opt |
min1 |
max2 |
|
Angle to line of sight 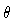 (degrees) (degrees) |
52.4 |
48.9 |
54.1 |
51.4 |
| Jet half-opening angles (degrees)3 |
|
|
|
|
inner region 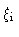 |
6.7 |
 |
 |
6.6 |
outer region  |
13.2 |
 |
 |
13.0 |
| Boundary positions (kpc) |
|
|
|
|
inner 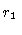 |
1.1 |
 |
 |
1.1 |
outer 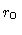 |
3.5 |
 |
 |
3.6 |
arbitrary fiducial 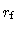 |
9.6 |
 |
 |
9.8 |
| Spine half opening angles (degrees) |
|
|
|
|
inner region 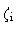 |
4.06 |
3.1 |
6.5 |
 |
outer region 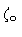 |
2.79 |
0.7 |
4.5 |
 |
On-axis velocities / 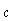 |
|
|
|
|
inner jet 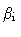 |
0.87 |
0.83 |
0.93 |
0.20 |
inner boundary 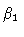 |
0.77 |
0.68 |
0.83 |
0.76 |
outer boundary 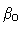 |
0.55 |
0.45 |
0.63 |
0.54 |
outer fiducial 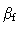 |
0.28 |
0.25 |
0.33 |
0.27 |
velocity exponent 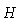 |
9.5 |
3.6 |
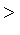 |
8.8 |
| Fractional velocity at edge of jet4 |
|
|
|
|
inner jet 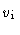 |
0.06 |
0.0 |
1.15 |
 |
inner boundary 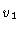 |
0.74 |
0.4 |
1.30 |
0.97 |
outer boundary 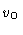 |
0.67 |
0.51 |
0.87 |
0.63 |
| On-axis emissivity exponents |
|
|
|
|
inner spine 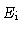 |
1.96 |
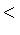 |
2.3 |
 |
flaring spine 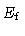 |
2.52 |
1.9 |
2.9 |
 |
outer spine 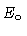 |
2.14 |
1.4 |
3.8 |
 |
inner shear layer 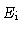 |
1.33 |
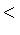 |
2.2 |
0.75 |
flaring shear layer 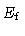 |
3.10 |
2.9 |
3.4 |
3.08 |
outer shear layer 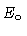 |
1.42 |
1.33 |
1.54 |
1.44 |
| |
|
|
|
|
| Fractional emissivity at edge of jet |
|
|
|
|
inner boundary 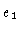 |
0.27 |
0.05 |
0.52 |
0.37 |
outer boundary 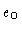 |
0.20 |
0.09 |
0.28 |
0.26 |
| |
|
|
|
|
| Shear layer / spine emissivity |
2.11 |
1.5 |
3.1 |
 |
| ratio at inner boundary |
|
|
|
|
| |
|
|
|
|
| Emissivity ratio at inner boundary |
|
|
|
|
| (inner / flaring region) |
|
|
|
|
spine  |
0.37 |
0.13 |
0.53 |
 |
shear layer  |
0.04 |
0.003 |
0.08 |
0.05 |
|
- 1 The symbol
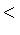 means that any value smaller
than the quoted maximum is allowed. means that any value smaller
than the quoted maximum is allowed.
- 2 The symbol
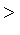 means that any value larger than the
quoted minimum is allowed. means that any value larger than the
quoted minimum is allowed.
- 3 Opening angles and boundary locations are given in the jet
coordinate system. The jet opening angles and the boundary locations are
determined by the outer isophotes once the angle to the line of sight is
specified , so
no errors are quoted.
- 4 The upper limits on the fractional velocity at the edge of the jet in
the inner region and at the inner boundary are set not by the
 constraint but rather by the condition that the velocity must be
constraint but rather by the condition that the velocity must be
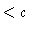 . .
|
Table 7:
Fitted parameters and error estimates (continued).
| |
|
|
|
|
| Quantity |
SSL |
Gauss |
| |
opt |
min |
max |
|
| |
|
|
|
|
| RMS field ratios (shear layer)5 |
|
|
|
|
| |
|
|
|
|
| radial/toroidal |
|
|
|
|
inner jet centre 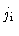 |
0.37 |
0.0 |
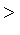 |
0.38 |
| inner jet edge |
0.0 |
|
|
0.0 |
inner boundary centre 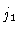 |
0.93 |
0.3 |
1.4 |
0.78 |
inner boundary edge 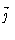 |
0.0 |
|
|
0.00 |
outer boundary centre 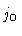 |
1.00 |
0.52 |
1.38 |
0.92 |
| outer boundary edge |
0.0 |
|
|
0.00 |
fiducial distance centre 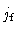 |
0.0 |
0.0 |
0.62 |
0.24 |
| fiducial distance edge |
0.0 |
|
|
0.00 |
index 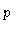 |
0.53 |
0.3 |
1.5 |
0.41 |
| longitudinal/toroidal |
|
|
|
|
inner jet 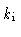 |
1.23 |
0.2 |
2.3 |
1.43 |
inner boundary 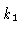 |
1.16 |
1.05 |
1.35 |
1.17 |
outer boundary 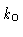 |
0.73 |
0.63 |
0.80 |
0.82 |
fiducial distance 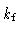 |
0.50 |
0.41 |
0.58 |
0.54 |
| |
|
|
|
|
| RMS field ratios (spine) |
|
|
|
|
| |
|
|
|
|
| radial/toroidal6 |
|
|
|
|
inner jet 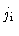 |
0.0 |
0.0 |
1.5 |
 |
inner boundary 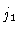 |
0.0 |
0.0 |
1.3 |
 |
outer boundary 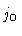 |
0.0 |
0.0 |
1.9 |
 |
fiducial distance 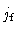 |
0.0 |
0.0 |
10.0 |
 |
| longitudinal/toroidal |
|
|
|
|
inner jet 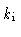 |
1.75 |
1.1 |
2.4 |
 |
inner boundary 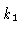 |
1.06 |
0.7 |
1.8 |
 |
outer boundary 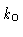 |
1.40 |
0.8 |
4.0 |
 |
fiducial distance 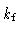 |
0.84 |
0.0 |
8.0 |
 |
| |
|
|
|
|
|
- 5 The
radial/toroidal ratios always vary from 0 at the spine/shear-layer
interface (SSL) or axis (Gaussian) to a maximum value at the edge of the
jet (Table 5).The values quoted are for the edge
and centre of the shear layer.
- 6 radial/toroidal field ratios for the spine in the SSL models are
consistent with 0 but poorly constrained everywhere (to the extent of
having negligible influence on the
 values). The relevant
parameters were fixed at 0 throughout the optimization process. values). The relevant
parameters were fixed at 0 throughout the optimization process.
|
Table 7 gives the fitted parameters and error estimates for the
spine/shear layer and Gaussian models. The parameters are the angle to the
line of sight, the spine opening angles and those defined in
Tables 4 - 5. The columns are:
- A description of the parameter. The symbols are those used in
Tables 4 - 5.
- The best fit for the SSL model
- The minimum value allowed by the
 recipe given earlier,
again for the SSL model.
recipe given earlier,
again for the SSL model.
- The corresponding maximum value.
- The best fit for the Gaussian model (the allowed ranges are very
similar to those for the SSL model).
In general, the parameters for the Gaussian and SSL models are very
similar and always agree within the quoted errors - the contribution of
the spine component to the emission (and therefore to the  value)
is quite small.
value)
is quite small.

![]() statistic is effective in optimizing the fit, but assessing
confidence limits (e.g. by a Bayesian analysis or using bootstrap
techniques) would be far from straightforward. We have instead adopted a
simple ad hoc procedure, by which we vary a single parameter until the
fractional increase in the
statistic is effective in optimizing the fit, but assessing
confidence limits (e.g. by a Bayesian analysis or using bootstrap
techniques) would be far from straightforward. We have instead adopted a
simple ad hoc procedure, by which we vary a single parameter until the
fractional increase in the ![]() values for I or Q and U in
one of the inner, flaring or outer regions corresponds to the formal
99% confidence limit for independent Gaussian errors and the appropriate
number of degrees of freedom. Most parameters affect the fit
significantly only for part of the jet, or for a subset of the Stokes
parameters, so this approach is superior to one based on the total
values for I or Q and U in
one of the inner, flaring or outer regions corresponds to the formal
99% confidence limit for independent Gaussian errors and the appropriate
number of degrees of freedom. Most parameters affect the fit
significantly only for part of the jet, or for a subset of the Stokes
parameters, so this approach is superior to one based on the total
![]() . The estimates are qualitatively reasonable, in the sense that
varying a parameter by its assigned error leads to a visibly unacceptable
fit, and we believe that they give a good general impression of the range
of allowed models. The numerical confidence levels should not be taken
too seriously, however.
. The estimates are qualitatively reasonable, in the sense that
varying a parameter by its assigned error leads to a visibly unacceptable
fit, and we believe that they give a good general impression of the range
of allowed models. The numerical confidence levels should not be taken
too seriously, however.