5.2 The onset of flaring and deceleration

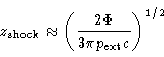
We have shown that the onset of deceleration is marked by a large increase in rest-frame emissivity and a major change in the jet collimation. It is not merely that the jet becomes gradually brighter as it decelerates and Doppler suppression is reduced: there is also a discontinuity at the inner boundary.

One possibility is that the jet is supersonic, over-pressured and expanding freely in the inner region. In that case, the internal pressure would fall until it drops below that of the external medium, at which point a reconfinement shock forms (Sanders 1983). The reconfinement shock is followed by a second shock at which the jet becomes overpressured with respect to the external medium and it this feature which is most plausibly identified with the flaring point. For a relativistic jet, Komissarov 1994 shows that the shock forms at a distance

$$z_{\rm shock} \approx \left ( \frac{2 \Phi}{3 \pi p_{\rm ext} c} \right )^{1/2}$$

where $\Phi$ is the energy flux through the jet and $p_{\rm ext} \approx 3 \times 10^{-11}$Pa (Hardcastle et al. , ) is the external pressure. This would be consistent with the observed inner boundary distance of 1.1kpc for an energy flux of $\approx 5 \times 10^{37}$W, somewhat higher than that the value of $\approx 1 \times 10^{37}$W estimated by 2002 () from a conservation-law analysis.

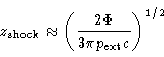
We see no evidence for any simple shock structure at the inner boundary, although the emission there is not completely resolved and there are obvious (non-axisymmetric) knots at the beginning of the flaring region. If the inner region is in free expansion, we can estimate the initial Mach number of the flow from the opening angle: $\arctan(\xi_{\rm i}) \approx {\cal M}$ where ${\cal M} = (\Gamma\beta)/(\Gamma_s\beta_s)$ is the generalized Mach number defined by Königl 1980, $\beta_s = c_s/c$, $c_s$ is the internal sound speed, and $\Gamma_s = (1-\beta_s^2)^{-1/2}$. The observed value of $\xi_{\rm i} = 6.7^\circ$ corresponds to ${\cal M} \approx 8.5$ and hence to $\Gamma \approx 6.1$ if the inner jet has the sound speed $c_s = c/\sqrt 3$ of an ultra-relativistic gas. This initial velocity is considerably faster than we have inferred for the inner region but, as mentioned in Section 5.1, we cannot exclude the presence of such higher-velocity material there.

A second possibility which has frequently been discussed in the literature is that the flaring point marks the onset of turbulence, or the position at which Kelvin-Helmholtz instabilities become non-linear (e.g. Begelman 1982 ; Bicknell 1986 ; Baan 1980 ; Rosen et al. 1999 ; De Young 1996 ; Bicknell 1984 ; Rosen & Hardee 2000).

We will show elsewhere (Laing & Bridle 2002) that conservation-law analysis favours the hypothesis that the flaring point is associated with a stationary shock, primarily because it suggests that the jet is over-pressured at the beginning of the flaring region. This does not, of course, exclude the subsequent development of entrainment (and presumably turbulence), as we now discuss.

2002-06-13