5.1 The inner region

Our estimates of the angle to the line of sight and the jet velocity in the inner region are entirely consistent with those of Lara et al. 1997 for the jets on parsec scales. For our preferred value of $\theta$ , their velocity range is $0.81 \leq \beta \leq 0.998$ , consistent with our central velocity for the inner region ( $\beta \approx 0.87$ ), but also allowing significant deceleration from parsec to kiloparsec scales.

The inner region poses a problem for any decelerating-jet model, in which the jet-to-counterjet intensity ratio (sidedness) must decrease with distance from the nucleus. We would expect the sidedness ratio to have a maximum in the inner region, in which case the counter-jet would be invisible. In fact, the inner region clearly has a lower sidedness, on average, than that in the flaring region. The brightness distribution is dominated by a few knots, so one possibility is that we are being fooled by stochastic variations. Alternatively, there could be a small amount of relatively slow-moving material in the shear layer, surrounding a fast spine.

If a very slow component also exists further out, it cannot have a noticeable effect on the brightness distribution: the fact that the sidedness ratio at the edges of the jet in the flaring region differs significantly from unity requires that the emissivity of any very slow component becomes insignificant on large scales. This component therefore has a negligible effect on the fits beyond the inner jet, and its properties are constrained only by the intensity fits in the inner region. The faster component of the flow that dominates the outer jets is relatively faint in the inner region (because its Doppler factor and intrinsic emissivity are both lower than on larger scales), so the modelling of the inner region is almost decoupled from that of the rest of the jets in the spine/shear-layer fits.

In the best fit SSL model, the slow component has been introduced by assigning a velocity of 0.06

to the shear layer while the spine has a velocity of 0.87

, i.e. we have allowed the slow component in the inner region to substitute for the faster-moving shear layer component that is required to explain the flaring region via an unphysical jump condition at the boundary. We emphasize that higher resolution imaging of the inner jets is needed to obtain firmer constraints on the transverse velocity distribution in this region, and to explore how this distribution evolves as the jet enters the flaring region.

**Figure 22:** A sketch of one possible geometry for the inner region and its transition to the flaring region, incorporating a slow boundary layer which does not persist at large distances from the nucleus.
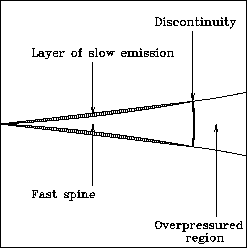$\begin{figure}\epsfxsize =7cm \epsffile{sketchin.eps}\end{figure}$

Our best guess at the geometry is sketched in Fig. 22. If this picture is correct, there must still be an increase in emissivity at the flaring point, but the values of

quoted in Table 7 will be inaccurate. Finally, we note that an additional component with $\beta$ significantly higher than 0.9 would be severely Doppler-dimmed even in the approaching jet, and therefore very difficult to detect.