Fractals and Astronomy
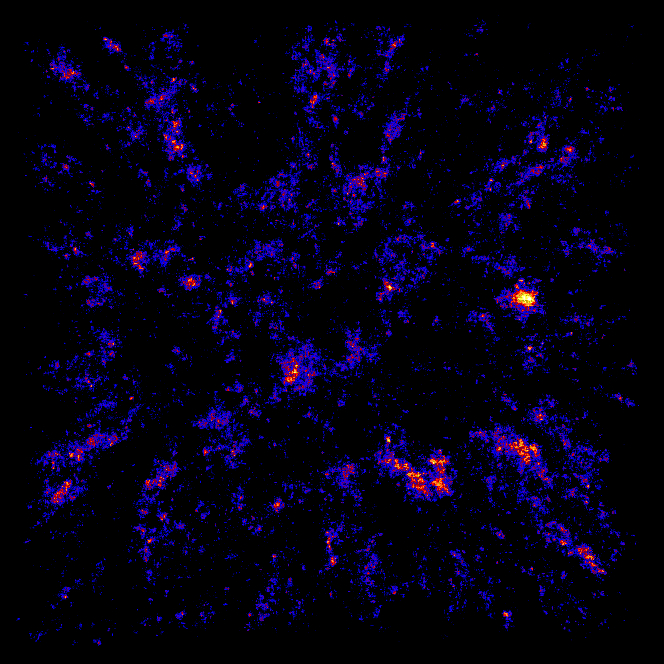
Peebles (1980) states that: "Given a random galaxy in a location, the correlation function describes the probability that another galaxy will be found within a given distance." People are also interested in the fractalization of the galaxy distribution in the Universe (out to a certain scale length). Cellular automata uses a fascinating computational technique that can take relatively simple rules to compute phenomena resulting in complex behavior. The figure I created at right is a projection of a 3D set of galaxies projected onto a 2D plane using the stochastic techniques outlined in Vicsek and Szalay (1987).
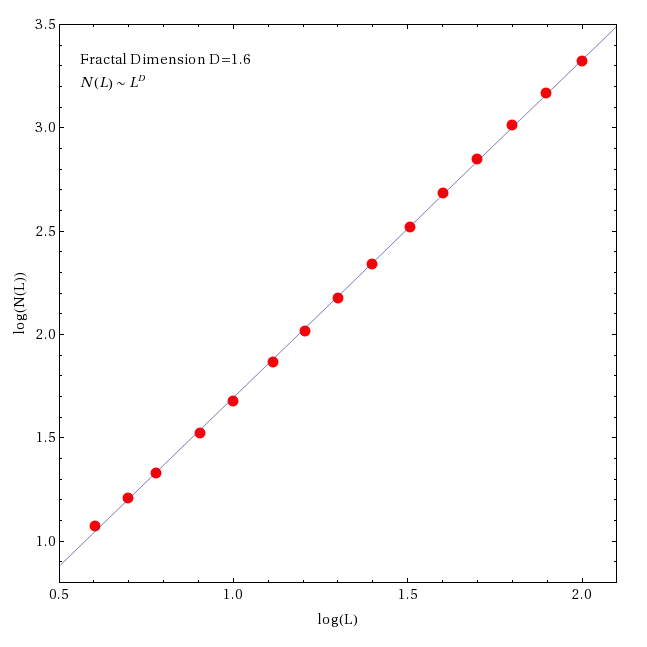
One can examine the fractal dimension of the simulated image by comparing the number of occupied cells in a grid within a box of size L. The resulting computation is best fit by a power law relation N(L) ~ LD. The least squares fit to the data shown in the figure at right gives a fractal dimension D=1.6. The figure and statistics were created with Mathematica. See the book by Heck and Perdang (1991) for a nice overview of fractal studies in astrophysics.
Interesting topics for study:
- What rules in cellular automation can result in different fractal dimensions? Vicsek and Szalay (1987) showed that various fractal dimensions would result based on certain threshold values being placed in the simulated data cubes.
- Does the resulting fractal dimension correlate with any observed cluster or galaxies parameters, i.e. cluster richness, morphology, galaxy color, etc.
- Do the resulting simulated galaxy fields created from various rule sets tell us anything about cluster properties as a function of redshift?
- What other scientific applications can this method be applied to?