Next: Asteroseismology-Observing for a SONG
Previous: Non-parametric Algorithms in Data Reduction at RATAN-600
Up: Algorithms
Table of Contents - Index - PS reprint
Astronomical Data Analysis Software and Systems VI
ASP Conference Series, Vol. 125, 1997
Editors: Gareth Hunt and H. E. Payne
Irina B. Vavilova
Astronomical Observatory of the Kiev University,
Observatornaya str., 3, Kiev 254053 Ukraine,
E-mail: vavilova@rcrm.freenet.kiev.ua
Piotr Flin
Pedagogical University, Institute of Physics,
ul.Lesna 16, Kielce 25-509 Poland,
E-mail: sfflin@cyf-kr.edu.pl
Abstract:
The analysis of two-dimensional galaxy distribution in the
Jagiellonian Field (JF) was carried out by the wavelet
technique. The positions of galaxies were taken from
the Revised Jagiellonian Field Catalogue (RJFC) based on
digitized scans of the JF original photographic plates. We
discuss briefly the procedure of star/galaxy separation
applied by us to the RJFC, the algorithm and the first
results of mapping of the selected parts of the RJFC.
The region of the original Jagiellonian Field (JF) sky
survey (Rudnicki, Dworak, & Flin 1973) was selected by
Zwicky (Zwicky 1962) as a region which is enriched by
clusters of galaxies and contains a small number of the
brighter galaxies. The JF sky survey (photographic plates
in three colors with coordinates of center
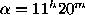 ,
, 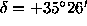 (2000.0)
taken with the 1.25m Palomar Schmidt telescope)
coincides with the CGCG field No. 185. The central
part of the JF (
(2000.0)
taken with the 1.25m Palomar Schmidt telescope)
coincides with the CGCG field No. 185. The central
part of the JF (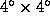 ) was scanned and
automatically processed by the COSMOS machine. This
procedure allows one to digitize the images on the plate and
to receive a set of parameters fitting the inertia ellipse
to each image (e.g., Stobie 1980; MacGillivray & Stobie 1984).
) was scanned and
automatically processed by the COSMOS machine. This
procedure allows one to digitize the images on the plate and
to receive a set of parameters fitting the inertia ellipse
to each image (e.g., Stobie 1980; MacGillivray & Stobie 1984).
Constructing a modern complete galaxy catalogue in the JF
region, we decided to carry out an automated procedure
of star/galaxy separation on the digitized images.
We experimented with the possible combinations of
parameters usually applied for such purposes on similar
photographic data (e.g., Hewett 1981; Heydon-Dumbleton,
Collins, & MacGillivray 1989; Odewahn et al. 1992; Weir,
Fayyad, & Djorgovski 1995 with a brief review of discrimination
philosophy).
Before applying the procedure, all small objects with
the COSMOS area parameter smaller than 60 (in increments)
were removed from our sample and about 35,000 objects remained to
be analyzed.
Among the possible discriminators only three
gave a clear separation of the loci of stars and galaxies. There
were plots presenting the dependence on the logarithm of
image area denoted as 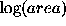 , the width of Gaussian
fit (S) and the intensity weighted second moment (
, the width of Gaussian
fit (S) and the intensity weighted second moment (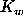 )
versus COSMOS image magnitude parameter COSMAG:
)
versus COSMOS image magnitude parameter COSMAG:
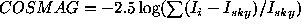 ,
where
,
where 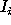 and
and 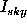 are the
intensity of i-pixel of the image and the intensity of the sky at the
image centroid respectively.
are the
intensity of i-pixel of the image and the intensity of the sky at the
image centroid respectively.
For bright and intermediate magnitudes we used
the log(area) vs. COSMAG discriminator. Due
to lower surface brightness for this range of magnitudes,
the galaxies lie above the stellar sequence on this plane.
For the intermediate magnitudes we applied the intensity
weighted second moment discriminator 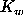 giving an
estimate of the filling of
the image by an ellipse fitted to its semiaxes:
giving an
estimate of the filling of
the image by an ellipse fitted to its semiaxes:
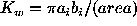 , where
, where 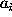 and
and 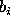 are the
intensity weighted semi-major and semi-minor
axes of the inertia ellipse respectively.
The more centrally concentrated images (stars) have the
smallest values of this parameter and occupy a tight locus
under the galaxy sequence.
are the
intensity weighted semi-major and semi-minor
axes of the inertia ellipse respectively.
The more centrally concentrated images (stars) have the
smallest values of this parameter and occupy a tight locus
under the galaxy sequence.
For the fainter and intermediate objects we used
the width of a best Gaussian fit (S) to the
threshold intensity and maximum image intensity:
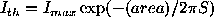 ,
where
,
where 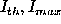 are the threshold
and maximum image intensity respectively. On this
diagram the Gaussian width for stars is determined by the
point spread function; galaxies lie above this sequence.
are the threshold
and maximum image intensity respectively. On this
diagram the Gaussian width for stars is determined by the
point spread function; galaxies lie above this sequence.
We checked all the brightest objects by visual inspection.
The principal point of the automated star/galaxy classification
is: the statistical weight of stars exceeds that of
galaxies for the whole range of considered magnitudes, and
stars occupy the tighter sequence for each discriminator
mentioned above. Therefore, for each magnitude in this
range, it is possible to construct the histogram of
distribution of the number of objects corresponding to the value of
chosen discriminator. This histogram gives the main points
for a spline to separate the star and galaxy sequences on
the plot of discriminator. Notice that, for intermediate
magnitudes, the loci of stars and galaxies are more separated,
so we did a spline interactively.
So, the Revised Jagiellonian Field Catalogue (RJFC) is based
on the digitized scans of the original JF photographic
plates. The RJFC contains information on about 20,000 galaxies
(Flin & Vavilova 1997, in preparation).
Modern astronomical data such as, e.g., DPS and digitized POSS
II surveys, constitute an excellent base for finding
large-scale structures. This structure search must be
objective, which requires appropriate mathematical methods.
The wavelet technique, being well-suited for approximation
of data with sharp discontinuities, seems to be one such
promising tool. For this reason we decided to verify the
applicability of the wavelet analysis, having at our
disposal data similar to DPS data, by carrying out the mapping
of a small region of the sky.
Unlike Fourier analysis, the wavelet algorithms process
data at different scales (resolutions). In the case of
applying the wavelets for detachment of the structure of
galaxy cluster, the task is to convolve the two dimensional
galaxy distribution ( signal function, 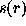 ) on a grid of
N×N pixels by the analyzing wavelet
) on a grid of
N×N pixels by the analyzing wavelet 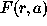 , where
a denotes the scale of the wavelet. This parameter determines
an effective radius of wavelet or, in other words, the extent of
spreading of the density distribution of galaxies in space of wavelet
coefficients (WC). So, such convolution leads to the ``spread''
galaxy distribution in terms of a wavelet, and
the further analysis of this distribution
can be performed using just the corresponding WC.
Adapting the best analyzing function
, where
a denotes the scale of the wavelet. This parameter determines
an effective radius of wavelet or, in other words, the extent of
spreading of the density distribution of galaxies in space of wavelet
coefficients (WC). So, such convolution leads to the ``spread''
galaxy distribution in terms of a wavelet, and
the further analysis of this distribution
can be performed using just the corresponding WC.
Adapting the best analyzing function
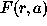 to data or cutting the WCs
below a threshold we sparsely represent our data.
to data or cutting the WCs
below a threshold we sparsely represent our data.
From the whole RJFC we chose small regions containing Abell
clusters: A1226, A1228, and A1257, two of them never studied
before. For the galaxy distribution in these three regions the
analyzing wavelet 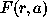 known as the ``Mexican Hat'' was
adopted. Avoiding the edge effects where discontinuities
occur, we analyzed a region greater than the cluster
itself. The ``Mexican Hat'' function has a radial shape
permitting however the detection of non-circular structure:
known as the ``Mexican Hat'' was
adopted. Avoiding the edge effects where discontinuities
occur, we analyzed a region greater than the cluster
itself. The ``Mexican Hat'' function has a radial shape
permitting however the detection of non-circular structure:
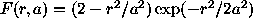 ,
where r is the distance between center
and point
,
where r is the distance between center
and point 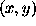 in which the ``Mexican Hat'' is calculated.
This approach has already been described and performed for
identification of structure of clusters of galaxies (e.g.,
Slezak, Bijaoui, & Mars 1990; Escalera et al. 1994).
in which the ``Mexican Hat'' is calculated.
This approach has already been described and performed for
identification of structure of clusters of galaxies (e.g.,
Slezak, Bijaoui, & Mars 1990; Escalera et al. 1994).
Our procedure had several principal steps:
- (i)
- normalizing the galaxy distribution data in the working zone
of the wavelets through a linear transformation into the range
[-1, 1], so the radius of the analyzed zone is
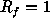 ;
;
- (ii)
- applying the ``Mexican Hat'' formula to the
normalized data;
- (iii)
- using a full set of scale wavelet
parameters: the analysis starts at the largest scale
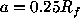 , where the structure of the whole cluster is
detected, and ends at the smallest one, where only one galaxy
is located inside the region;
, where the structure of the whole cluster is
detected, and ends at the smallest one, where only one galaxy
is located inside the region;
- (iv)
- performing a Monte-Carlo simulation using the same
number of galaxies, distributed in the same zone,
to verify the reality of detected structures and substructures;
- (v)
- picking up the galaxies inside the detected structure
of the cluster to study the properties of galaxy cluster.
The first results of mapping of the RJFC gave additional
support for the correctness and efficiency of the wavelet analysis
both for detachment of the structure of galaxy clusters itself
and for the further investigation of their morphological
properties (Flin & Vavilova 1995, 1996).
Notice that, in our case,
the existence of the structures had been known a
priori and the task here was to adapt the analyzing function.
The problem of finding the structure of the
galaxy cluster and the galaxy group (e.g., with low richness,
having different geometrical scales, and lying close to
each other in two- or three-dimensional space)
in a general distribution is not easy. For mapping the
general galaxy distribution in the whole RJFC, some other
families of wavelet systems and approaches should be applied.
It looks as if, in this case, it would be correct to use a hierarchical
algorithm, sometimes called a pyramidal algorithm
(e.g., Bijaoui 1996, private, communication), providing the multiscale vision of
a sky survey like the RJFC.
Acknowledgments:
IBV thanks the ADASS VI Organizing Committee for the
financial support enabling her to participate in so exciting
and fruitful conference, as well as Pedagogical University
in Kielce for hospitality during her stay there.
References:
Escalera, E., Biviano, A., Girardi, M., Giuricin, G.,
Mardirossian, F., Mazure, A., & Mezzetti, M. 1994, ApJ,
423, 539
Flin, P., & Vavilova, I. B. 1995, SISSA Ref. 65/95/A,
ed. G. Giuricin, F. Mardirossian, M. Mezzetti
Flin, P., & Vavilova, I. B. 1996, Astrophys. Letters &
Communications, to be published
Hewett, P. 1981, report for internal distribution ROE
Heydon-Dumbleton, N. H., Collins, C. A., &
MacGillivray, H. T. 1989, MNRAS, 238, 379
MacGillivray, H. T., Stobie, R. S. 1984, Vistas in
Astron., 27, 4, 433
Odewahn, S. C., Stockwell, R. L., Pennington, R.
M., Humphreys, R. M., & Zumach, W. A. 1992, AJ, 103, 318
Rudnicki, K., Dworak, T. Z., & Flin, P. 1973,
Acta Cosmologica, 1, 7
Slezak, E., Bijaoui, A., & Mars, G. 1990, A&A,
227, 301
Stobie, R. S. 1980, JBIS, 33, 323
Weir, N., Fayyad, U., & Djorgovski, S. 1995, AJ,
109, 2401
Zwicky, F. 1962, in Problems of Extra-galactic
Research, ed. G. C. McVittie (New York: Macmillan),
347
© Copyright 1997 Astronomical Society of the Pacific,
390 Ashton Avenue, San Francisco, California 94112, USA
Next: Asteroseismology-Observing for a SONG
Previous: Non-parametric Algorithms in Data Reduction at RATAN-600
Up: Algorithms
Table of Contents - Index - PS reprint
payne@stsci.edu
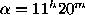 ,
, 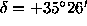 (2000.0)
taken with the 1.25m Palomar Schmidt telescope)
coincides with the CGCG field No. 185. The central
part of the JF (
(2000.0)
taken with the 1.25m Palomar Schmidt telescope)
coincides with the CGCG field No. 185. The central
part of the JF (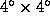 ) was scanned and
automatically processed by the COSMOS machine. This
procedure allows one to digitize the images on the plate and
to receive a set of parameters fitting the inertia ellipse
to each image (e.g., Stobie 1980; MacGillivray & Stobie 1984).
) was scanned and
automatically processed by the COSMOS machine. This
procedure allows one to digitize the images on the plate and
to receive a set of parameters fitting the inertia ellipse
to each image (e.g., Stobie 1980; MacGillivray & Stobie 1984).
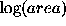 , the width of Gaussian
fit (S) and the intensity weighted second moment (
, the width of Gaussian
fit (S) and the intensity weighted second moment (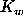 )
versus COSMOS image magnitude parameter COSMAG:
)
versus COSMOS image magnitude parameter COSMAG:
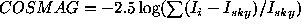 ,
where
,
where 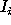 and
and 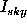 are the
intensity of i-pixel of the image and the intensity of the sky at the
image centroid respectively.
are the
intensity of i-pixel of the image and the intensity of the sky at the
image centroid respectively.
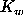 giving an
estimate of the filling of
the image by an ellipse fitted to its semiaxes:
giving an
estimate of the filling of
the image by an ellipse fitted to its semiaxes:
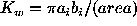 , where
, where 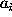 and
and 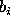 are the
intensity weighted semi-major and semi-minor
axes of the inertia ellipse respectively.
The more centrally concentrated images (stars) have the
smallest values of this parameter and occupy a tight locus
under the galaxy sequence.
are the
intensity weighted semi-major and semi-minor
axes of the inertia ellipse respectively.
The more centrally concentrated images (stars) have the
smallest values of this parameter and occupy a tight locus
under the galaxy sequence.
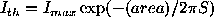 ,
where
,
where 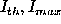 are the threshold
and maximum image intensity respectively. On this
diagram the Gaussian width for stars is determined by the
point spread function; galaxies lie above this sequence.
are the threshold
and maximum image intensity respectively. On this
diagram the Gaussian width for stars is determined by the
point spread function; galaxies lie above this sequence.
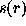 ) on a grid of
N×N pixels by the analyzing wavelet
) on a grid of
N×N pixels by the analyzing wavelet 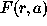 , where
a denotes the scale of the wavelet. This parameter determines
an effective radius of wavelet or, in other words, the extent of
spreading of the density distribution of galaxies in space of wavelet
coefficients (WC). So, such convolution leads to the ``spread''
galaxy distribution in terms of a wavelet, and
the further analysis of this distribution
can be performed using just the corresponding WC.
Adapting the best analyzing function
, where
a denotes the scale of the wavelet. This parameter determines
an effective radius of wavelet or, in other words, the extent of
spreading of the density distribution of galaxies in space of wavelet
coefficients (WC). So, such convolution leads to the ``spread''
galaxy distribution in terms of a wavelet, and
the further analysis of this distribution
can be performed using just the corresponding WC.
Adapting the best analyzing function
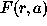 to data or cutting the WCs
below a threshold we sparsely represent our data.
to data or cutting the WCs
below a threshold we sparsely represent our data.
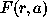 known as the ``Mexican Hat'' was
adopted. Avoiding the edge effects where discontinuities
occur, we analyzed a region greater than the cluster
itself. The ``Mexican Hat'' function has a radial shape
permitting however the detection of non-circular structure:
known as the ``Mexican Hat'' was
adopted. Avoiding the edge effects where discontinuities
occur, we analyzed a region greater than the cluster
itself. The ``Mexican Hat'' function has a radial shape
permitting however the detection of non-circular structure:
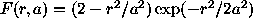 ,
where r is the distance between center
and point
,
where r is the distance between center
and point 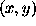 in which the ``Mexican Hat'' is calculated.
This approach has already been described and performed for
identification of structure of clusters of galaxies (e.g.,
Slezak, Bijaoui, & Mars 1990; Escalera et al. 1994).
in which the ``Mexican Hat'' is calculated.
This approach has already been described and performed for
identification of structure of clusters of galaxies (e.g.,
Slezak, Bijaoui, & Mars 1990; Escalera et al. 1994).
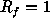 ;
;
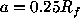 , where the structure of the whole cluster is
detected, and ends at the smallest one, where only one galaxy
is located inside the region;
, where the structure of the whole cluster is
detected, and ends at the smallest one, where only one galaxy
is located inside the region;