4.1.1 values

**Table 6:** Summary of reduced $\chi ^2$ values.
Model type	No blanking	Arc blanked
SSL	1.71	1.51
Gaussian	1.80	1.60

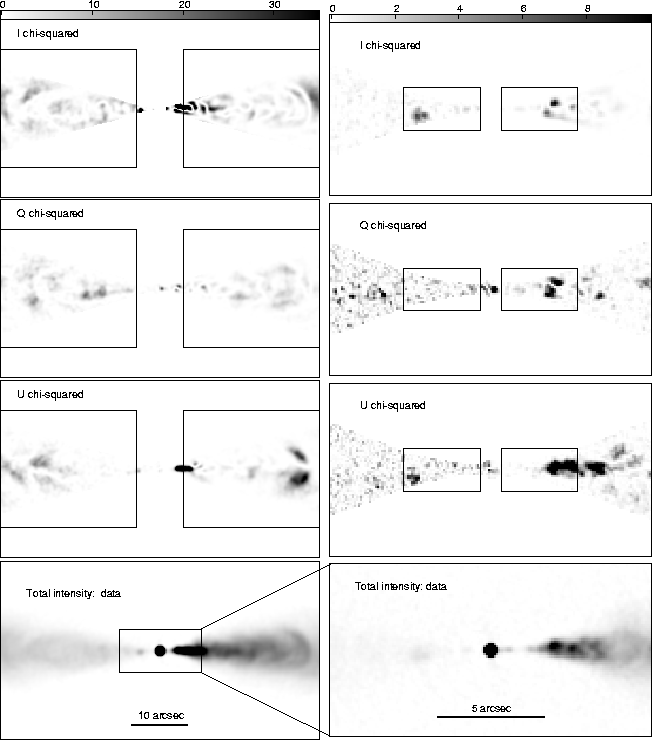
We have optimized models with spine/shear layer and Gaussian transverse profiles. The resulting reduced $\chi ^2$ values, with and without blanking of the brightest arc in the main jet, are given in Table 6 and images of $\chi ^2$ are shown in Fig. 5. Both models fit the large-scale total intensity and polarization distributions well. Given that the ``noise levels'' are crudely estimated (and likely to be too low), and that the ``noise'' shows large-scale correlation with clearly non-Gaussian statistics, it is not unexpected that the reduced $\chi^2 \approx$ 1.5-1.8 is inconsistent with a formal fit.

**Figure 5:** Grey-scale images of $\chi^2 = (S_{\rm model}-S_{\rm observed})^2/\Sigma^2$ ,
where $\Sigma$ is the ``noise level'' defined in the text.

Left: images with a resolution of 0.75 arcsec FWHM covering an area of ± 27 arcsec from the nucleus. Right: images with 0.25 arcsec FWHM of the inner ± 7.5 arcsec. The labelled bars indicate the grey-scale ranges: these are different for the two resolutions. The boxes show the areas over which $\chi ^2$ was summed at each resolution to assess goodness of fit.
From the top: $\chi ^2$ images for Stokes I, Q and U; total intensity for the same area. $\chi ^2$ values are not plotted for Stokes I in the immediate vicinity of the core.
$\begin{figure}\epsfxsize =17cm \epsffile{chisqmosaic.eps}\end{figure}$

In what follows, we concentrate on the SSL model as the best description of velocity, emissivity and field ordering regardless of the underlying physics. The Gaussian equivalent has a smaller number of free parameters (Table 7). It gives a slightly, but significantly worse fit, except in the inner region, where it fails seriously (albeit with little effect on the overall $\chi ^2$ ).