5.4 The emissivity profile and adiabatic models

We have determined the variation of $n_0 B^{1+\alpha }$ (proportional to the emissivity) in the rest frame of the emitting material. Separation of this variation into particle and field contributions requires additional assumptions. The X-ray emission from the jets (Hardcastle et al.2002) is most likely to be synchrotron, rather than inverse Compton radiation, so we cannot use it to decouple the particle and field components. We therefore postpone a discussion of the variation of pressure and density along the jet to Laing & Bridle (2002), where we also consider X-ray observations of the surrounding hot gas.

A number of authors (Baum et al.1997, Feretti et al.1999; Bondi et al.2000) have recently re-opened the possibility that the jets in FRI radio galaxies are adiabatic in the sense first defined by Burch (1979), i.e. that the particles suffer only adiabatic energy losses, there are no dissipative processes causing particle acceleration or field amplification and the magnetic field is convected passively with the flow. We defer a full discussion of this question to a later paper, since our data and models are both substantially more complicated than is allowed by the analytical approaches in the literature (Baum et al.1997). The simplest adiabatic models do not allow for any turbulent flow (Section 5.3) and there is independent evidence for particle acceleration in 3C31's jets from X-ray observations (Hardcastle et al.2002). Nevertheless, we can make a number of preliminary qualitative points.

We take the analytical formulae from Baum et al. (1997). In the absence of velocity shear and in the quasi-one-dimensional approximation, the field components vary as:

$$\begin{eqnarray*} B_l & \propto & x^{-2} \\ B_t & \propto & (x\beta\Gamma)^{-1} \\ B_r & \propto & (x\beta\Gamma)^{-1} \\ \end{eqnarray*}$$

where x is the jet radius. For a purely longitudinal field, this leads to a variation of the rest-frame emissivity:

  $$\begin{eqnarray*} \epsilon & \propto & (\Gamma\beta)^{-(2\alpha+3)/3}x^{-(10\alpha+12)/3} \\ & = & (\Gamma\beta)^{-1.37}x^{-5.83} \\ \end{eqnarray*}$$

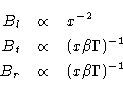
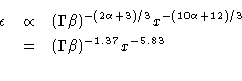
and for a perpendicular field ($B_l = 0$):

$$\begin{eqnarray*} \epsilon & \propto & (\Gamma\beta)^{-(5\alpha+6)/3}x^{-(7 \alpha+ 9)/3} \\ & = & (\Gamma\beta)^{-2.92}x^{-4.28} \\ \end{eqnarray*}$$

The inner region poses a severe problem for the simplest adiabatic models: we have no evidence for deceleration so, if the conical region is fully filled, we would expect a very rapid brightness decline away from the nucleus ( $\propto z^{-4.28}$ on-axis even in the perpendicular-field case) compared with our estimates of $\propto z^{-1.96}$ for the spine and $\propto z^{-1.33}$ for the shear layer. Even for the steepest emissivity fall-off allowed by our error analysis (Table 7), the indices are grossly discrepant. We have already argued that much of the emission in the inner region may come from a surface layer (Section 5.1) and the assumption that the radiating material expands with constant opening angle may be invalid.

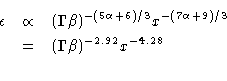
For the flaring and outer regions, we have computed the emissivity variations for the parallel- and perpendicular-field cases using our model for the radius and velocity of the jet. The results are shown in Fig. 17, where we have normalized the adiabatic models to the observed emissivities at the beginnings of the flaring and outer regions. Two example streamlines are shown for the SSL model: on-axis in the spine and at the inner edge of the shear layer. The adiabatic models predict emissivities which fall far more rapidly than is observed in the flaring region: the deceleration is too little and too late to compensate for the expansion. In the outer region, by contrast, the perpendicular-field adiabatic model predicts emissivities fairly close to those observed.

There are two other fundamental problems with the adiabatic models. First, the field structure in the flaring region is not consistent with passive convection in a smooth, axisymmetric velocity field. Our assumed velocity field acts so as to shear an existing radial component, thereby amplifying the component along the flow. It cannot, therefore, create the region of approximately isotropic field at the edge of the flaring region starting with what is essentially a mixture of toroidal and longitudinal components. Second, the assumed velocity field cannot change the ratio of radial to toroidal field. It is clear from Fig. 21 that the radial component essentially disappears at some point after the flaring region.

We conclude that simple adiabatic models could not describe the inner and flaring regions, even if more realistic field configurations and the effects of velocity shear were to be included, but that a model of this type may apply to the outer region, at least if the radial field component is mostly eliminated by the outer boundary. Further investigation of this set of problems is outside the scope of the present paper and will be presented elsewhere.

2002-06-13