6  3C31 at other angles to the line of sight

The best-fitting spine/shear-layer models require the jets to be at 52$^\circ$ to the line of sight.

Figure 23: The best-fitting model of the 3C31 jets viewed at various angles $\theta$ to the line of sight with a beam of 0.75arcsec FWHM. 

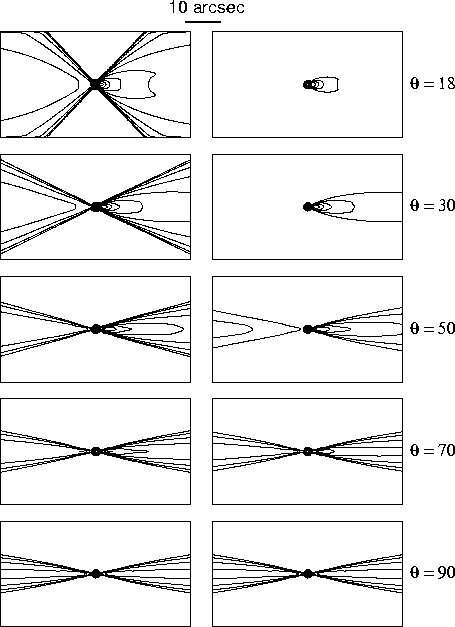Fig. 23 shows the appearance of these models if observed with the jet axis at other angles to the line of sight at a resolution of 0.75arcsec. We have not modelled the core, but need to make a crude estimate of the dependence of its flux density on $\theta$ in order to illustrate the effects of observing with limited dynamic range. For these calculations the effective flow velocity in the core has been arbitrarily set at $\beta = 0.95$ ($\Gamma = 3.2$) and its flux is assumed to scale with angle according to the predictions of a simple single-velocity model for a pair of oppositely directed, identical jets:

$$S_{\rm c} \propto [\Gamma(1-\beta\cos\theta)]^{-(2+\alpha_c)} + [\Gamma(1+\beta\cos\theta)]^{-(2+\alpha_c)}$$

The spectral index of the core, $\alpha_c = 0$. The models are shown for $\theta$=90$^\circ$ (jet axes in the plane of the sky), then for $\theta$ decreasing in 20$^\circ$ steps to 30$^\circ$. The final model is shown at $\theta$=18$^\circ$ as this is close to the limiting case that our code can compute, wherein the line of sight lies inside the widest cone angle subtended by the jet outflow at the nucleus (in the flaring region).

The left panels show how the jets would appear if they could be observed at these angles to the line of sight with the same limiting sensitivity as in our VLA data for 3C31, using logarithmically spaced contours.

Figure 24: The best-fitting model of the 3C31 jets viewed at various angles $\theta$ to the line of sight with a beam of 0.25arcsec FWHM. Left panel: logarithmic contours with fixed sensitivity, i.e. with the same lowest contour in all plots. Right panel: logarithmic contours with fixed 2048:1 dynamic range i.e. with the same percentages of the peak intensity in all plots. Both sets of plots cover $\pm$10arcsec from the nucleus and the angular scale is indicated by the bar at the top of the diagram.

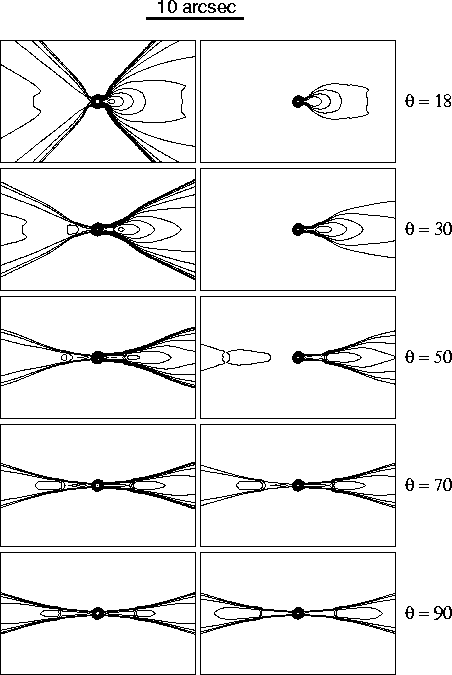Fig. 24 shows a similar display for an observing resolution of 0.25arcsec FWHM, emphasizing the changes in appearance of the inner jet and the start of the flaring region.

The $\theta$=90$^\circ$ case is, of course, symmetrical with two identical centre-brightened jets that lack well-defined intensity maxima at their bases. Images of 3C449 (Feretti et al.1999) and PKS1333$-$33 (Killeen, Bicknell & Ekers 1986) show precisely these features.

At $\theta$=70$^\circ$, we see the effects of moderate differences in the Doppler boost between the two sides: the base of the main jet appears brighter, and the counter-jet is both dimmer and less centrally-peaked than the main jet (compare 3C296; Hardcastle et al. 1997 ). At $\theta$=50$^\circ$, we see essentially the symmetries observed in 3C31's jets. Note that the counter-jet brightens on an absolute scale at lower inclination angles $\theta$ because each line of sight now intersects a longer absolute path length through both jets. At $\theta$=30$^\circ$, the bright base of the main jet is effectively contiguous with the unresolved core, and at $\theta$=18$^\circ$ the characterization of the structure as a ``jet" according to the usual criteria (Bridle & Perley 1984) would be questionable at this resolution. By $\theta$=18$^\circ$, the apparent flux density of the core has also increased from 0.03 Jy at $\theta$=90$^\circ$ to 1.6 Jy. This makes it unlikely that the wide-angle emission from the outer layers of the jet would be detected except in observations specifically designed for high dynamic range (or low angular resolution).

The right panels illustrate this by plotting the same five models with logarithmically spaced contours at fixed percentages of the apparent peak intensity, to a limit of 1/750 of the peak. The contours are chosen to match the appearance of the left panel for the $\theta$=90$^\circ$ case. These ``constant dynamic range'' displays probably correspond better to ``standard'' radio astronomical observations that have not been specially optimized to detect faint broad features in the presence of strong compact components. For $\theta$=30$^\circ$ and $\theta$=18$^\circ$, most of the emission detected outside the compact core comes from close to the spine of the approaching jet. Images of BL Lac objects such as 3C371 (Wrobel & Lind 1990; Pesce et al. 2001) and Mkn501 (Conway & Wrobel 1995) show qualitatively similar features, although the effects of projection exaggerate deviations from axisymmetry.

Figure 25: The best-fitting model of the 3C31 jets viewed at various angles $\theta$ to the line of sight. Vectors whose lengths are proportional to the degree of polarization and whose directions are those of the apparent magnetic field are superimposed on selected total intensity contours. 

Fig. 25 shows the variation of polarization with angle at two different resolutions. The relative separation of the parallel-perpendicular apparent field transitions in the main and counter-jets from the nucleus is a strong function of inclination. For the main jet, the transition point moves away from the nucleus into the flaring region as $\theta$ drops from 90 to 45$^\circ$, despite the opposite effect of projection on the position of the flaring point. As $\theta$ decreases still further, the transition moves closer to the nucleus again. In contrast, the field transition in the counter-jet moves monotonically closer to the nucleus as $\theta$ decreases, with the parallel-field region being essentially invisible for $\theta \leq 30^\circ$. The longitudinal apparent field at the edges of the jets also becomes less prominent as $\theta$ increases, and would be difficult to detect for $\theta \approx$ 90$^\circ$ in observations with limited sensitivity. Both effects are inevitable consequence of the toroidal/longitudinal field structure. We expect them to be general features of FRI sources, testable for complete samples even where detailed modelling is impossible because of intrinsic asymmetry or low signal-to-noise. There is little published data on field transition distances, but 3C296 (Hardcastle et al. 1997) and 0755+379 (Bondi et al. 2000) indeed have transition points further from the nucleus in their main jets.

Figs 23-25 explicitly demonstrate the possibility of generating a variety of apparent FRI jet structures with the same physical model by varying the orientation and of unifying FRI radio galaxies with some classes of ``one-sided'' objects. They also illustrate the need for careful consideration of observational selection effects when analysing statistical properties of unified models. In the presence of a range of flow velocities both along and across every jet, observational selection through limited sensitivity and dynamic range translates into velocity selection within the jets. A key byproduct of our models may be a way to guide the statistical interpretation of jet velocities in blazar-FRI unification models, as discussed by Laing et al.(1999).

The analysis of jet sidedness and width ratios for a complete sample by Laing et al. (1999) shows that our models are likely to apply in detail to the inner parts of the majority of FRI jets (i.e. before bending and other intrinsic effects become dominant). The results of Laing et al. (1999) suggest that some model parameters vary systematically from source to source: in particular, the length of the inner region and the characteristic scale of deceleration appear to increase with radio luminosity

2002-06-13